What is $\inf_{n \in \mathbb{N}} n \times\Big($ distance to nearest integer of $n\sqrt{2}\Big)$?

Question

I am invested of a simpler variation of the Littlewood conjecture, for a specific value, namely $\sqrt{2}$.

The problem

To begin, we define the function $f(x)$ for a real value $x$ as the distance from $x$ to the integer closest to it. Or written more formally:

$$f(x) = |x - \lfloor x \rceil| = |x - \text{round}(x)| = \min_{n\in Z} |x - n|$$

where $\lfloor x \rceil = \text{round}(x)$ is the round to integer "function" (Wikipedia doesn't call it a function, but functions for the process exist in language like Python, so I put that in quotes).

The problem: Calculate the following: $$\inf_{n \in \mathbb{N}, \ n \geq 1} \ (n \times f(n\sqrt{2}))$$

where the condition $n \geq 1$ is given to prevent the case $n = 0$, which just makes the product zero.

---

Some theoretical work

$\sqrt{2}$ has irrational measure $2$, which means that there are infinitely many pairs of integers $(p, q)$ such that

$$ 0 < \left|\sqrt{2} - \frac{p}{q}\right| < \frac{1}{q^2} $$

Define a sequence $(q_i)_{i=1}^\infty$ such that all $q_i$ has a $p_i$ that satisfy the upper equation together (that is, for each $q_i$, there exists a corresponding $p_i$ such that

$$0 < \left|\sqrt{2} - \frac{p_i}{q_i}\right| < \frac{1}{{q_i}^2}$$

and the $q_i$ are increasing. (Well, there are infinitely many of them, so just find and sort, I guess, but it doesn't really matter).

Now, let $e_i = \left|\sqrt{2} - \frac{p_i}{q_i}\right|$. As the $q_i$ gets larger, the $e_i$ tends to zero due to the squeeze theorem. At this point, let's try to substitude the number $q_i$ into the $n \times f(n \sqrt{2})$. We have:

$$ q_i \times f(q_i \sqrt{2}) = q_i \times f\left(q_i \left(\frac{p_i}{q_i} + e_i\right)\right) = q_i \times f(p_i + q_ie_i) $$

Assume that $q_i$ is extremely large, which makes $\frac{1}{q_i}$ small and $\frac{1}{{q_i}^2}$ even smaller. Since $e_i$ is bounded between $0$ and $\frac{1}{{q_i}^2}$, this would also make $e_i$ really, impossibly small. If we assume that both $e_i$ and $\frac{1}{{q_i}^2}$ are too small for them to have any meaningful difference, then we assume $e_i \approx \frac{1}{{q_i}^2}$ and we have:

$$ q_i \times f(p_i + q_ie_i) \approx q_i \times f\left(p_i + q_i \frac{1}{{q_i}^2}\right) \\ = q_i \times f\left(p_i + \frac{1}{q_i}\right) \approx q_i \times \frac{1}{q_i} = 1??? $$

(I put the question marks at the end because I'm not sure, and I felt like there are mistakes somewhere, but oh well)

But now, that is not the craziest part...

---

Some numerical work.

Instead of using the massive theoretical work above, I implement a piece of Python code to check over all $n \times f(n\sqrt{2})$ in a range from $1$ to some number. Here, I pick $10^7$.

def f(a: float) -> float:
    return math.fabs(a - round(a))
def L(n: int) -> float:
    return n * f(n * math.sqrt(2))
t = 10 ** 10 # some big value
z = 0
for i in range(1, 10 ** 7 + 1):
    if L(i) <= t:
        z = i
        t = L(i)
print(z)
print(t)

Here, L(n) represents the value of the formula $n\times f(n\sqrt{2})$, z represents the index n where we met the smallest value of L(n), which is n * f(n * math.sqrt(2)), while t denotes the actual value itself. So here's what surprising.

print(z) prints $2$. At $z = 2, t = 0.343145\dots$.

I did not expect the value to appear so early.

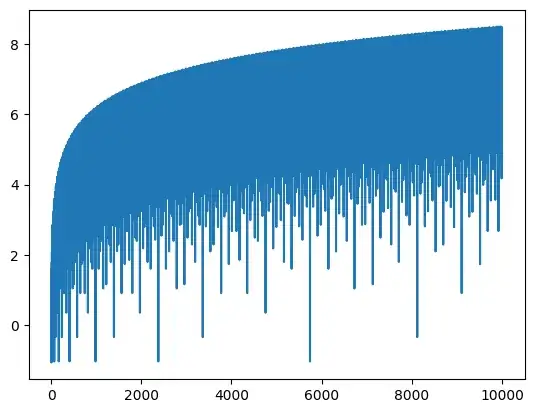
I also plotted the sequence $\log L(n)$ with $n$ from $0$ to $10^4$ as follows:

x = np.arange(1, 10001)
y = np.array([math.log(L(i)) for i in x])
y
plt.plot(x, y)

And this is the resulting image:

It's definitely interesting to see the dips, but I still can't believe the first dip appeared so early though.

What do you think?

Answer 1

The minima are associated with "near-integer" cases described by

$(1+\sqrt2)^m=a_m+b_m\sqrt2\tag{1}$

where $a_m/b_m$ may be recognized as continued fraction approximants to $\sqrt2=[1;\overline2]$. For example, the minimum just below $6000$ is actually at $n=5741$, which matches (1) with $m =11$.

Then we have the conjugate relation

$(1-\sqrt2)^m=a_m-b_m\sqrt2\tag{2}$

From (1) and (2) we derive:

$b_m=\frac{1}{2\sqrt2}[(1+\sqrt2)^m-(1-\sqrt2)^m]$

and the closest integer to $b_m\sqrt2$ is

$a_m=\frac{1}{2}[(1+\sqrt2)^m+(1-\sqrt2)^m].$

We then have

$b_m|a_m-b_m\sqrt2|=\frac12[1-(-1)^m(1-\sqrt2)^{2m}],$

where we have $1/(1+\sqrt2)=-(1-\sqrt2)$ to eliminate $1+\sqrt2$ from the product.

Then as $m\to\infty$ the powers of $1-\sqrt2$ strictly oscillate to zero and therefore the local minima tend to $1/2$. It follows that the global minimum is a local minumum below $1/2$ for some finite $m$ and thus finite $n=b_m$.

The product is below $1/2$ when $m$ is even, and the smallest available $m$ giving the largest magnitude of the power of $1-\sqrt2$ is $m=2$. This then gives $n=b_2=2$ and the resulting product value $6-4\sqrt2\approx0.3431$.

Answer 2

Markov constant for $\sqrt 2$ is $2 \sqrt 2$ - so there is number $M > 0$ s.t. $\left| \sqrt 2 - \frac pq\right| > \frac{M}{q^2}$ for all $p, q$.

Then $f(n \sqrt 2) = \left|n\sqrt 2 - p\right| = n \left|\sqrt 2 - \frac pn\right| \geq \frac{nM}{n^2} = \frac{M}{n}$. Thus $n \cdot f(n\sqrt 2) \geq M$ for all $n$, and also $\inf n \cdot f(n \sqrt 2) > 0$.