Let $ABC$ be a planar triangle.
Consider a random line $L$ in the plane, non parallel to any of the sides of the triangle, intersecting line $BC$ in $P$, line $AC$ in $Q$ and line $AB$ in $R$.
Question : what is the locus of points
$$G=\frac13(P+Q+R) \ \tag{0}$$
(center of weights of the 3 points) when line $L$ is varying ?
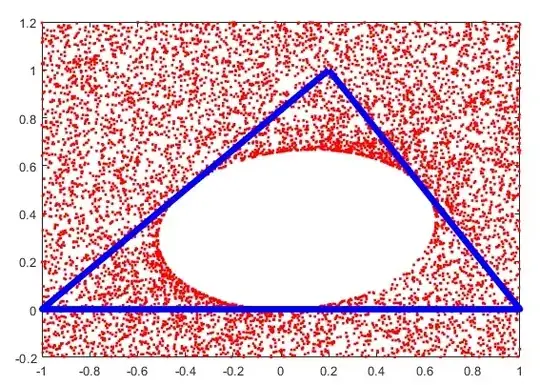
$$\textit{Fig. 1 : Many different points $G$ : none is inside}$$
$$\textit{the Steiner inellipse of ABC.}$$
I have an analytical answer (see proof below).
My question : is it possible to have a geometrical proof ?
My answer :
Let the barycentric coordinates of $P,Q,R$ wrt triangle $ABC$ be :
$$\begin{cases}P&(&0,&p,&(1-p)&),\\Q&(&(1-q),&0,&q&)\\R&(&r,&(1-r),&0&)\end{cases}\tag{1}$$
(where $p,q,r$ can be positive or negative).
As $P,Q,R$ are aligned, we have ;
$$\det\pmatrix{0&(1-q)&r\\p&0&(1-r)\\(1-p)&q&0}=0\tag{2}$$
which is equivalent to :
$$(1-p)(1-q)(1-r)=-pqr\tag{2'}$$
or to :
$$r=\frac{(1-p)(1-q)}{1-p-q}\tag{2''}$$
Remark : $(2),(2'),(2'')$ are different ways to express Menelaus theorem under its signed version.
Point $G$ defined by (0) has the following barycentric coordinates :
$$G \begin{cases}x&=&(1-q+r)/3,\\ y&=&(1-r+p)/3,\\z&=&(1-p+q)/3\end{cases}\tag{3}$$
(one can check that the sum of these bar. coord. is $1$).
Let us consider the following polynomial with barycentric coordinates equation (i.e., with $x+y+z=1$) :
$$f(x,y,z)=x^2+y^2+z^2-2(xy+yz+zx)\tag{3}$$
We have (see here) :
$$f(x,y,z) \begin{cases}&=&0&\text{"Steiner inellipse"} \ S_I.\\&\le&0&\text{interior of} \ S_I.\\&\ge&0&\text{exterior of} \ S_I. \end{cases}\tag{4}$$
($S_I$ is the ellipse internally tangent to the sides of $ABC$ in their midpoints).
If we "plug" the coordinates of $G$ given by (3) into the equation of $S_I$, taking into account the expression (2'') of $r$, we get :
$$f(x,y,z)=\underbrace{\frac{(p^2+q^2+pq-2p-2q+1)^2}{(1-p-q)^2}}_{ \ge 0}\tag{5}$$
As a consequence of (4), the generic point $G$ is always situated at the exterior of $S_I$.
We can conclude that the locus of points $G$ is exactly the exterior of $S_I$ because the exterior of $S_I$ is covered by ellipses $E_k$ with equations :
$$f(x,y,z)=k$$
where $k$ is any positive constant, which are homothetic images of ellipse $S_I$, the center of homothety being the centroid. For example, taking $k=1$, we obtain the outer Steiner ellipse, circumscribed to triangle $ABC$.