Find side length of a right triangle with a square sitting inside.

Question

Problem statement:

Let $\triangle ABC$ be a right triangle with $B=\frac{\pi}{2}$ and a unit square sitting inside the triangle as shown in the image below. Find the length of the side $AB$

The only solution I could think of was:

By the Pythagorean theorem $$AB^2=AC^2-BC^2\iff(y+1)^2+(x+1)^2=4^2$$ Notice that by the slope of the hypotenuse we get $\frac1x=\frac y1\iff xy=1$. The problem becomes equivalent to solving the quartic : $$x^4+2x^3-14x^2+2x+1=0$$

My question: Is there any other way to solve this that doesn't involve solving a fourth degree equation?

Thanks to anyone who took the time to read.

Answer 1

You have: $(y+1)^2 + (x+1)^2 = 4^2$

Expand out:

$y^2 + x^2 + 2y + 2x + 2 = 4^2$

Since you have $xy=1$, you can set $2=2xy$:

$y^2 + x^2 + 2y + 2x + 2xy = 4^2$ $\implies (y + x)^2 + 2(x+y) = 4^2$

Let $k = (y+x)$; solve the quadratic in $k$ (taking the positive solution): $k = \sqrt{17} - 1$

Hence $x+y = (\sqrt{17} - 1)$; substituting $y=\frac{1}{x}$ you have a quadratic in $x$ to solve.

Answer 2

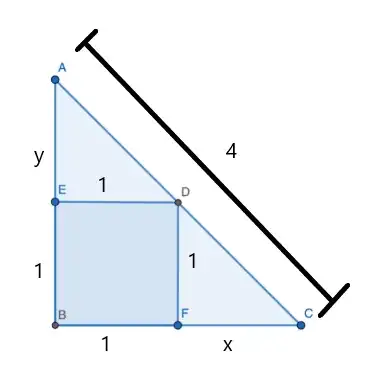
Alternative approach:

The equation

$$x^4+2x^3-14x^2+2x+1=0, \tag1 $$

can be directly converted into a quadratic equation by recognizing that the equation in (1) above is a symmetric quartic equation. That is, the $~x^4~$ and $~x^0~$ coefficients are equal, and the $~x^3~$ and $~x^1~$ coefficients are equal.

Therefore, the method employed in this answer may be used.

First, the equation in (1) above is transformed into

$$\left( ~x^2 + \frac{1}{x^2} ~\right) + 2\left( ~x + \frac{1}{x} ~\right) - 14 = 0. \tag2 $$

Then, you set $~w = \displaystyle \left( ~x + \frac{1}{x} ~\right),~$ and note that
$\displaystyle w^2 - 2 = \left( ~x^2 + \frac{1}{x^2} ~\right).$

Therefore, the equation in (2) above becomes

$$( ~w^2 - 2) + 2w - 14 = 0 \implies w^2 + 2w - 16 = 0 \implies $$

$$w = \frac{1}{2} \left[ -2 \pm \sqrt{ ~4 + 64 ~} ~\right] = -1 \pm \sqrt{17}.$$

Since $~w = \displaystyle \left( ~x + \frac{1}{x} ~\right),~$ which must be positive, the negative root above must be rejected.

Therefore,

$$w = \left( ~x + \frac{1}{x} ~\right) = -1 + \sqrt{17} \implies $$

$$x^2 + x \left( ~1 - \sqrt{17} ~\right) + 1 = 0 \implies $$

$$x = \frac{1}{2} \left[ ~\sqrt{17} - 1 \pm \sqrt{~18 - 2\sqrt{17} - 4 ~} \right]$$

$$= \frac{1}{2} \left[ ~\sqrt{17} - 1 \pm \sqrt{~14 - 2\sqrt{17} ~} \right]. \tag3 $$

What the equation in (3) above represents is that there are $~2~$ different solutions, depending on whether $~x < y,~$ or $~y < x.$

---

$\underline{\text{Sanity Checking}}$

The solution given in (3) above may be routinely sanity checked to verify that both of the following constraints are satisfied:

• $xy = 1.$

• $(x + 1)^2 + (y+1)^2 = 4^2 = 16.$

$$\left\{ ~\frac{1}{2} \left[ ~\sqrt{17} - 1 + \sqrt{~14 - 2\sqrt{17} ~} \right] ~\right\} \\ \times \left\{ ~\frac{1}{2} \left[ ~\sqrt{17} - 1 - \sqrt{~14 - 2\sqrt{17} ~} \right] ~\right\} $$

$$= \frac{1}{4} \left\{ ~ \left[ ~18 - 2\sqrt{17} ~\right] - \left[ ~14 - 2\sqrt{17} ~\right] ~\right\} = \frac{4}{4}.$$

Note that $~(R + S)^2 + ~(R - S)^2 = 2(R^2 + S^2).$

Therefore,

$$\left\{ ~\frac{1}{2} \left[ ~\sqrt{17} + 1 + \sqrt{~14 - 2\sqrt{17} ~} \right] ~\right\}^2 \\ + \left\{ ~\frac{1}{2} \left[ ~\sqrt{17} + 1 - \sqrt{~14 - 2\sqrt{17} ~} \right] ~\right\}^2 $$

$$= 2 \times \frac{1}{4} \times \left\{ ~\left[ ~18 + 2\sqrt{17} ~\right] + \left[ ~14 - 2\sqrt{17} ~\right] ~\right\}$$

$$= \frac{2}{4} \times (18 + 14) = 16.$$

Answer 3

Another way to solve leads to a quartic too and it is because of the unknowns are irrational of four degree. For example we have $$x^2+1=(2+h)^2\\y^2+1=(2-h)^2\\xy=1$$ which yields $$(h^2+4h+3)(h^2-4h+3)=1\implies h^4-10h^2+8=0$$ or $$(h^2-5)^2-17=0$$ so we can make $$\overline{AD}=2-\sqrt{5-\sqrt{17}} \text{ and }\overline{DC}=2+\sqrt{5-\sqrt{17}}$$ In this case the resultant equation is simpler than yours but it is also irreducible over $\mathbb Q$ and the unknowns are of the four degree. You can verify that solutions of your quartic are also irrational of the four degree.

Answer 4

Couldn't you just use simple observational geometry, and the Pythagorean Theorem?

If $BEDF$ is a unit square, then $AED$ and $DFC$ are both right triangles of the same size. And that means point $D$ lies in the center of line $AC$, given by sheer geometry: angle $ADE$ must equal the angle $DCF$, and $CDF$ must equal $DAE$, since every right triangle's angles add up to $180°$, line $ADC$ is $180°$, and angle $EDF$ is $90°$ (unit SQUARE) no matter how long $x$ or $y$ are.

Since $AED$ is a right triangle, and $D$ is the midpoint of $AC$ (making line $AD$ , $2$ units long), then you have a Pythagorean Theorem:

$$y^2 + 1^2 = 2^2$$

Simplifying this, you get:

$$y^2 = 4 - 1 = 3$$

$$y = \sqrt{3}$$

Since $y$ is the length of line $AE$, and you're given the length of line $EB$ as $1$ unit, then the length of line $AB$ is $\left(1 + \sqrt{3}\right)$ units

Answer 5

The two triangles are similar. y=1/x=p/q (two hypotenuses) So y=p/q and p+q=4 p-qy=0, q(y+1)=4 1<q<3 (hypotenuse) So y(1/3;3) Analogical for x