3

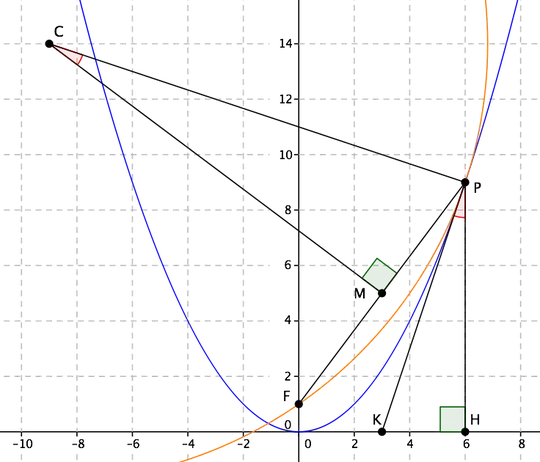
Finding the equation of a circle touching a parabola $x^2=4y$ at the point $(6,9)$ and passing through its focus.

Let the center of the circle be $(h,k)$ and radius $r$, then its equation is

\begin{equation} (x-h)^2+(y-k)^2=r^2 \tag{1} \end{equation}

as it passes through $(0,1)$ and $(6,9)$ we have

\begin{equation} \begin{cases} h^2+(1-k)^2=r^2 \\ \\ (6-h)^2+(9-k)^2=r^2 \end{cases} \tag{2} \end{equation}

Subtraction these two we have

\begin{equation} 3h+4k=29 \tag{3} \end{equation}

The Eq. of tangent of the parabola at (6,9) is $3x=y+9$. And the perpendicular distance of this from $(h,k)$ equals the radius $r$, and we get

\begin{equation} \left|\frac{3h-k-9}{\sqrt{10}}\right|=r \tag{4} \end{equation}

By solving $(3)$ and $(4)$ and putting them in $(2)$, we get $h=-9,k=14, r=5\sqrt{10}$ and hence the circle $(1)$.

The question is am I missing an elegant solution?

Yunxuan Zhang
  • 1,344
Z Ahmed
  • 46,319

1 Answers1

4

Let $F=(0,1)$ be the focus and $P=(6,9)$ the given point; $H=(6,0)$ the projection of $P$ on the $x$-axis and $M=(3,5)$ the midpoint of $FP$.

The bisector of $\angle FPH$ cuts the $x$-axis at the midpoint $K=(3,0)$ between $H$ and the vertex of the parabola. The center $C$ of the circle lies on the perpendicular bisector of $FP$ and on the perpendicular to tangent $PK$ at $P$. Hence triangle $PMC$ is similar to triangle $KHP$: $$ CM:PM=PH:HK \quad\implies\quad CM=15. $$

Finding the coordinates of $C$ is then straightforward, because $(-4,3)/5$ is a unit vector perpendicular to $FM$: $$ C=M+15\cdot{(-4,3)\over5}. $$

enter image description here

Intelligenti pauca
  • 55,765
  • Nice! But I think there must be some property of that half-angle that I'm not familiar with. Perhaps more straightforward to say that the gradient of the parabola at $P$ is $3$, so the gradient of $CP$ is $-\frac13$? – TonyK Jan 20 '25 at 22:17
  • @TonyK Yes, you can also find $C$ as the intersection of perpendiculars $PC$ and $MC$, if you want. I prefer a more geometric reasoning. That $K$ is the midpoint of $VH$ is easy to understand if you look at the figure of the linked answer. – Intelligenti pauca Jan 21 '25 at 09:31