3

I have a basic question. Consider the function:

$$f(x) = \begin{cases} 1-x^2 & \text{if $x\le 0$, and} \\ x^2 & \text{if $x > 0$.} \end{cases}$$

This function is not continuous at $0$: $\lim_{x\to0^{-}} f(x) = 1$, but $\lim_{x\to0^{+}} f(x) = 0$. So it should not be differentiable at $0$.

But don't we also know both of the following facts:

$$\lim_{h\to 0^{-}}\dfrac{f(h)-f(0)}{h} = \lim_{h\to 0^{-}} -h = 0 \tag{1}$$

and

$$\lim_{h\to 0^{+}}\dfrac{f(h)-f(0)}{h} = \lim_{h\to 0^{-}} h = 0. \tag{2}$$

But then it follows that $\lim_{h\to 0}\frac{f(h)-f(0)}{h}$ exists, i.e. $f^{'}(0)$ exists. What am I missing?

Xander Henderson
  • 32,453
Stephen Schultheis
  • 39
  • 7
    Note that $f(0)=1$ holds whether you're doing the left difference quotient limit or the right difference quotient limit. – Dave L. Renfro Jan 20 '25 at 16:11
  • I still don't get it. f'(0) exists iff the left difference quotient limit equals the right difference quotient limit. We just showed that the left difference quotient limit equals the right difference quotient limit. So it follows that f'(0) exists, and f is differentiable at 0. But clearly f is not continuous at 0. So it would seem that differentiability does not imply continuity. Which step in this argument is wrong? – Stephen Schultheis Jan 20 '25 at 20:00
  • 3
    Equation (2) is wrong. We have $\frac{f(h)-f(0)}{h}=\frac{h^2-1}{h}=h-\frac{1}{h}$, which approaches $0-\infty=-\infty$ as $h\to 0^+$. – peek-a-boo Jan 20 '25 at 20:09
  • 1
    To add to what I said and @peek-a-boo said, you did not use the correct value for $f(0)$ for the right difference quotient limit. If you graph $y=f(x),$ you'll see that $f(0) = 1$ represents a single point on the graph, and that point is the same whether you look to the left of it or look to the right of it. Your error is a common beginning error and is a reasonably natural error to make, by the way. There is probably at least one question somewhere here that addresses it, but I don't have time to look now. And if not, a nice detailed answer by someone would be a useful addition to this site. – Dave L. Renfro Jan 20 '25 at 20:18
  • 1
    Clicking on "Tags" (top left of computer screen) and using the search word "piece", I found the tag "derivatives-of-piecewise-functions". More than likely, questions that are similar to your question can be found among the questions with that tag. – Dave L. Renfro Jan 20 '25 at 20:27

1 Answers1

2

I think this is quite a good question even if the reason $f’(0)$ is not defined is rather simple. As I’ll explain, your example does illustrate something fairly interesting.

Why $f’(0) \neq 0$:

Note that your definition of $f$ is

$$f(x) = \begin{cases} 1-x^2 & x \leq 0 \\ x^2 & x > 0 \end{cases}$$

So we have that $f(0)=1$.

Hence

$$\begin{align} \lim_{h \to 0^+} \left( \frac{f(h) - f(0)}{h} \right) &= \lim_{h \to 0^+} \left( \frac{h^2 - 1}{h} \right) \\ &= \lim_{h \to 0^+} \left(h - \frac{1}{h}\right) \end{align}$$

which is undefined (as $h \to 0^+$ this gets arbitrarily large.)

Your mistake is that you put $f(0)=0$ in this limit. I think your mistake is that you asserted $\lim_{h \to 0^+} f(h) = f(0)$ here, which isn’t necessarily the case, and isn’t the case for this $f$. The discontinuity of $f$ at $0$ occurs when approaching $0$ from the positive direction, hence why the this limit won’t be defined.

Your example is interesting:

But what you have observed, if I write $f(0^+)$ and $f(0^-)$ as shorthand for $\lim_{x \to 0^+} f(x)$ and $\lim_{x \to 0^-} f(x)$, that

$$\lim_{h \to 0^+} \left( \frac{f(h) - f(0^+)}{h} \right) = \lim_{h \to 0^-} \left( \frac{f(h) - f(0^-)}{h} \right) $$

Or alternatively, that $$\lim_{x \to 0^+} f’(x) = \lim_{x \to 0^{-}} f’(x).$$

What this means is that, while $f$ is discontinuous at $x=0$ and cannot be extended to a continuous function. However, $f’$ is discontinuous (in particular undefined at a point) but it can be extended to a continuous function. Formally, what I mean is that there does not exist a continuous function $g$ such that $g(x) = f(x)$ for $x \neq 0$, but there does exist a function $g$ such that $g(x) = f’(x)$ for $x \neq 0$ (namely, $g(0)=0$). Perhaps the easiest way to see this is from the graphs of $f$ and $f’$:

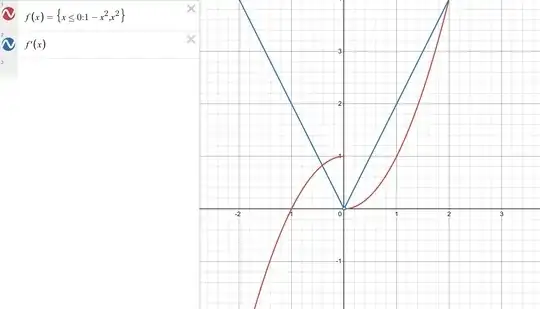
A graph of f and f’. f looks discontinuous whereas f’ looks continuous even though it is missing a point

(Image courtesy of Desmos, modified by me to emphasise the discontinuity)

To help emphasise this further, you might want to consider what the anti-derivative of a function which is continuous at all but a a few isolated points can look. Can you see how different intervals of the antiderivative could have different constants of integration, yet still be valid anti-derivatives? How does this relate back to our example?

Robin
  • 6,201