How many triangles can be formed by the points of a regular $25$-gon so that triangles do not share any side with that $25$-gon?

Question

problem: How many triangles can be formed by the points of a regular $25$-gon so that triangles do not share any side with that $25$-gon? Triangles are considered the same if they differ only by a rotation of the $25$-gon.

My approach:

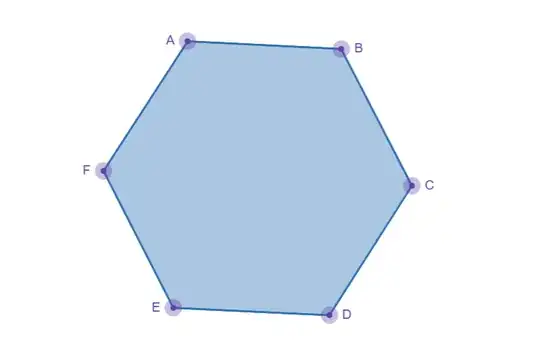
Let's consider a regular $6$ gon. Since, this a regular $6$ gon, it doesn't matter where we put the $1$st point. All will be equivalent. Let's say, our $1$st point is $A$. So, we can't put the $2$nd point in $B$ and $F$ otherwise, $AB$ and $AF$ will be a side of that polygon. We have $6-1-2=3$ choices.

$1$st case: We will not take common. Let's say, we will put the $2$nd point in $C$ or $E$. The points, we can't put the $3$rd point are $B$,$D$,$F$,$D$. $B$ is common by $A$ and $F$ is common by $A$. Now we don't want that. We will have $2$ common so $2$ points. So, $3-2=1$. Let's put $2$nd point. We have $1$ choice which is $D$. How many choices are left for the $3$rd point? $1-1=0$. Oh, no choices. So, no triangle.

$2$nd case: We will take common. Even though , we have $6-3=3$ choices, since $A$ have $2$ commons, if we want to have common, we have $2$ choices to put the $2$nd point. Let's say, we will put $2$nd point on $C$. $B$ is common. We have $6-1$($A$ point it self)-$2$($F$ and $B$)-$1$($C$ itself)-$1$($D$)=$1$. And that point is $E$.

Let's do it for $25$ gon. we will not take common first. We have $25-1-2=22$ choices for the $2$nd point. Since, we don't want common, we have $22-2=20$ choices. We have $1$ point $A$ others are the neighbor points($2$). Also, we have the $2$nd point.$2$nd point has 2 neighbors too. We have $25-1-2-1-2=19$ ways we can put the $3$rd point. The amount of triangles are $20*19=380$. If we have common, we have $2$ choices for the $2$nd point. We will choose one. Since, we have common, we have $25-1-2-1-1=20$ choices for the $3$rd point. The amount of triangle are $20*2=40$. In total, the amount of triangle are $380+40=420$.

Conclusion: This is quite tricky that's why I recommend to understand every line. I posted here to make sure that my solution is correct or not. Please, help me.

Answer 1

Looking clockwise, attach one unused vertex $\Large\bullet$ to each of the $3$ used vertices $\Large\circ$ that will form the triangle, viz. $\boxed{\Large{\circ\bullet}}$

Now there are $3$ boxes + $(25-6) = 22$ objects.

Place the boxes in $\binom{22}{3}$ ways,
but you are allowing boxes only $(22)$ starting places instead of $25$, so multiply by $\frac{25}{22}$ to get $\frac{25}{22}\times\binom{22}{3} =1750$

---

Addendum

I now get what you are asking for, so what you need to do is to $\texttt{totally fix}$ one vertex, say $1$ and count, so for a polygon of $25$ sides, you will have configurations like

• $1,3|5-24 = 20$
• $1,4|6-23 = 19$
• .........
• $1,21|23 = 1,\; total\; 210$

Trying to find the pattern, we get

• hexagon:$1$
• septagon:$3$
• octagon:$6$
• nonagon:$10$

and the formula that emerges for total # of distinct triangles, N, for a n-gon is

$$N = \sum_{i=1}^{n-5}i = \frac{(n-5)(n-4)}2$$

$\underline{\texttt{Simpler Solution}}$

There was so much conversation as to what is wanted, I see that the problem could have been solved in a jiffy.

Consider the gaps between unique triangles as $22$ "stars" to be put in $3$ non-empty "bins", then by stars and bars over positive integers, Theorem 1, we directly get the # of triangles as $$\binom{22-1}{3-1} =\binom{21}2 = 210$$

Generalised for a n-gon, $\dbinom{n-4}2$

Answer 2

Let's do it for an $n$-gon and then set $n=25$. We may assume $n\ge4$.

The number of triangles containing a given vertex is equal to the number of solutions of the equation $x+y+z=n-3$ in positive integers. By the "stars and bars" formula, that number is $\binom{n-4}2$. Multiply by $n$ since there are $n$ vertices, then divide by $3$ because each triangle has been counted $3$ times; the total number of triangles is $$T_n=\frac n3\binom{n-4}2=\frac{n(n-4)(n-5)}6.$$ So $T_4=T_5=0$, $T_6=2$, $T_7=7$, $T_8=16$, $T_9=30$, $T_{10}=50$, $T_{11}=77$, $T_{12}=112$, and $$T_{25}=\frac{25\cdot21\cdot20}6=1750.$$ See OEIS sequence A005581.

The above is the solution of the problem as it was originally stated. It transpires that you want the number of distinguishable triangles, where triangles are considered indistinguishable if they differ only by a rotation of the $n$-gon. Let $t_n$ be the number of distinguishable triangles.

If $n$ is not divisible by $3$ then $$t_n=\frac{T_n}n=\frac{(n-4)(n-5)}6;$$ in particular $$t_{25}=\frac{1750}{25}=70.$$ In general $$t_n=\left\lceil\frac{(n-4)(n-5)}6\right\rceil;$$ this is the number of necklaces with $3$ black beads and $n-6$ white beads (which is the same as th enumber of necklaces with $3$ black beads and $n-3$ white beads, no black beads being next to each other); see OEIS sequence A007997. The first few terms (from $n=4$ to $n=25$) are $$0,0,1,1,2,4,5,7,10,12,15,19,22,26,31,35,40,46,51,57,64,70.$$

Answer 3

Addendum added to respond to the comment question of Geometry99.

---

For the $~25~$ sided polygon, the easiest approach is to subtract the unsatisfactory triangles.

There are $~\displaystyle \binom{25}{3}~$ ways of forming a triangle, where the constraint against one of the sides of the triangle being a side of the polygon is ignored.

From this computation, you have to subtract the number of unsatisfactory triangles. This problem can be conquered by either Inclusion-Exclusion, or the direct approach.

See this article for an introduction to Inclusion-Exclusion. Then, see this answer for an explanation of and justification for the Inclusion-Exclusion formula.

The inclusion exclusion approach would be to let $~S~$ denote the entire set of possible triangles.

Then, assuming that the polygon's sides are indexed $~D_1, ~\cdots, ~D_{25},~$ you can let $~S_k~$ denote the subset of $~S~$ that represents that one of the sides of the triangle is $~D_k.$

So, you would want

$$| ~S ~| - | ~S_1 \cup ~\cdots \cup S_{25} ~|.$$

Then, you would employ the method in the linked articles, noting that you can't have more than $~2~$ of the polygon's sides in a single triangle, and noting that the number of ways of having $~2~$ of the polygon's sides in the same triangle is very limited.

---

In general, Inclusion-Exclusion is preferred, because it generalizes well. However, in this problem, I prefer the direct approach to enumerating the unsatisfactory triangles, because it is so simple.

For a triangle to share exactly one side with the polygon, there are $~25~$ possible sides. For each side chosen, the two neighboring points must be ignored, because then the polygon would share two sides, instead of only one side.

So, the partial enumeration of unsatisfactory triangles is $~(25 \times 21).$

For a triangle to share exactly two sides, there are $~25~$ ways of pairing up neighboring sides. Each such pairing determines the triangle.

So, the final computation is

$$\binom{25}{3} - (25 \times 21) - (25).$$

---

$\underline{\text{Addendum}}$

Responding to the comment question of Geometry99:

Where is the mistake in mine?

You correctly determined that any satisfying triangle in the hexagon would be congruent to $~\triangle ACE.~$ So, in the hexagon, there are $~2~$ such triangles.

Let's do it for $25$ gon. we will not take common first. We have $25-1-2=22$ choices for the $2$nd point. Since, we don't want common, we have $22-2=20$ choices. We have $20$-$2$(Where we can't put points.)=$18$. The amount of triangles are $20*18=360$. If we have common, we have $2$ choices for the $2$nd point. We will choose one. Since, we have common, we have $25-1-2-1-1=20$ choices for the $3$rd point. The amount of triangle are $20*2=40$. In total, the amount of triangle are $360+40=400$.

I am sorry. In order to diagnose your analysis, I first have to understand it. I do not understand the above paragraph. Perhaps some other MathSE reviewer will be able to understand and remedy your analysis, as it is currently written.

In order for me to understand the ideas that you are trying to express, you are going to have to overhaul your posting to clarify your thinking.

That is, you would need to strive to present your ideas in such a clear fashion that it is very difficult for anyone to be in any way confused about what you are trying to say.

Further, because your ideas seem to be so complicated, it would be a good idea to pick out examples, such as a $~10~$ sided polygon, a $~15~$ sided polygon, and the $~25~$ sided polygon.

As part of your clarification of your ideas, you could implement your algorithm, whatever it is, against each of these three examples, and very carefully detail all of your analysis, step by step, directly in the posted question.

This would facilitate my analyzing your posted question.