1

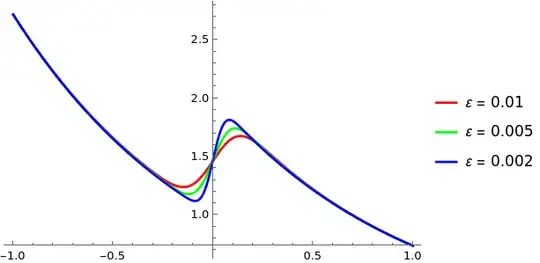
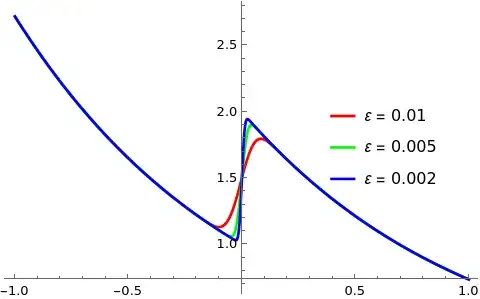
Background

Looking for an approximated uniform solution for:

$$\epsilon y''+xy'+xy=0, \quad y(-1)=e, \quad y(1)=\frac{2}{e}$$

enter image description here

I found the following

  1. Outer solutions: $$y^{outer}_{left}(x)=e^{-x},\quad y^{outer}_{right}(x)=2e^{-x}$$ enter image description here
  2. Matching at $$y^{match}_{left}=1,\quad y^{match}_{right}=2$$
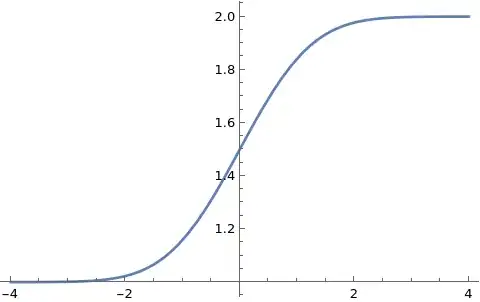
  3. Inner solutions: $$y_{inner}=\frac{1}{\sqrt{2\pi}}\int_0^\frac{x}{\epsilon}e^{-\frac{t^2}{2}}dt+\frac{3}{2}$$ enter image description here

Question

How to construct $y_{unif}$?

Attempt

This discussion seems to conclude that $$y_{\rm unif}=\frac{y_{\rm out}^{\rm left}+y_{\rm out}^{\rm right}}2+\left(y_{\rm in}-\frac{y_{\rm match}^{\rm left}+y_{\rm match}^{\rm right}}2\right) $$ However, plugging the above results, $y_{unif}$ seems to be wrong: $$y_{unif}(-1)=\frac{e+2e}{2}+1-\left(\frac{1+2}{3}\right)=1.5e$$ Since it is originally required that $y(-1)=e$, we find that: $$y(-1)\neq y_{unif}(-1)$$

Michael
  • 415
  • 2
  • 10
  • Your ODE corresponds to the case $p=-1$ in https://math.stackexchange.com/questions/4811787/leading-order-matching-of-epsilon-xpy-y-y-0?rq=1. The boundary conditions are not the same, but maybe you can adapt the answer to that question to your problem. – Gonçalo Jan 16 '25 at 15:22
  • Thanks @Gonçalo ! The main challenge for me is in finding the uniform solution for both sides of the origin. The referred question seems to discuss only one side of the origin with fixed value at the origin. So, I don't know how to deduct from that setup to mine. – Michael Jan 16 '25 at 15:33
  • 1
    (1) The upper limit of integration in $y_{inner}$ should be $\frac{x}{\epsilon^{1/2}}$ instead of $\frac{x}{\epsilon^{1/2}}$ (see Eq. (2) in https://math.stackexchange.com/a/4811999/1163258). (2) The expression for $y_{unif}$ in the post that you cite is valid if $y_{out}^{right}-y_{out}^{left}=\text{const.}$, which is not true in your case. Instead, I suggest that you use $y_{unif}=y_{out}^{left}+(y_{out}^{right}-y_{out}^{left})(y_{inner}-1)$. Later I'll write an answer to justify my suggestion. – Gonçalo Jan 17 '25 at 04:37
  • @Michael It seems to me, that you didn't do a matching, but rather a patching... – ASlateff Jan 17 '25 at 07:18
  • @ASlateff what do you mean? Step 2 above is a derivation of $\lim_{\xi \to \infty} y_i = \lim_{x \to 0} y_O$ as described in the Matching section of this wiki page. – Michael Jan 17 '25 at 07:27
  • @Gonçalo that should work, as the step function would enforce the right solution in every region. Thanks. – Michael Jan 17 '25 at 07:29
  • I'll check a similar term to the one @Gonçalo suggested: $y^{outer}{left} (y{match}^{right}-y_i)+y^{outer}{right}(y_i-y{match}^{left})$. – Michael Jan 17 '25 at 07:40

2 Answers2

1

In the spirit of @Gonçalo's comment, this seems a good solution: $$y^{outer}_{left} (y_{match}^{right}-y_i)+y^{outer}_{right}(y_i-y_{match}^{left})$$ Plot of the solution

The boundary layer width seems different, but that's another story.

Michael
  • 415
  • 2
  • 10
0

This is not in the spirit of the question.

I faced a very similar problem years ago and, adapting to your equation, I give a solution (forgetting the conditions).

Let $$y (x)=z(x)\,\exp\Bigg(x \left(1-\frac{x}{2 \epsilon }\right) \Bigg)$$ which gives $$\epsilon\, z''-(x-2\epsilon)\,z'-(1-\epsilon)\,z=0$$ which is an Hermite differential equation.

Assuming $\epsilon>0$, let $t=\frac{x-2 \epsilon }{\sqrt{2\epsilon }}$ the solution is then $$ z= c_1\, H_{\epsilon -1}(t)+c_2 \, _1F_1\left(\frac{1-\epsilon }{2};\frac{1}{2};t^2\right)$$ where appear Hermite polynomial and Kummer confluent hypergeometric function.

The given conditions lead to messy expressions for $c_1$ and $c_2$ but your first plots are perfectly reproduced.

Claude Leibovici
  • 289,558