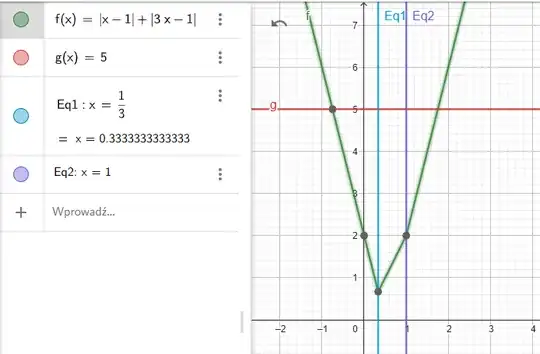
Solve $|x-1|+|3x-1|=5$

Question

Solve $|x-1|+|3x-1|=5$

By definition of absolute value:

$|x-1|=\begin{cases} -x+1, &\text{if $x<1$} \\ \ \ \ x-1, &\text{if $x \geq1$} \end{cases}$

$|3x-1|=\begin{cases} -3x+1, &\text{if $x<\frac{1}{3}$} \\ \ \ \ 3x-1, &\text{if $x \geq \frac{1}{3}$} \end{cases}$

For $x<\frac{1}{3}$: $|x-1|+|3x-1|=5 \Rightarrow(-x+1)+(-3x+1)=5 \Rightarrow x=\frac{-3}{4}$

For $\frac{1}{3} \leq x < 1$:$|x-1|+|3x-1|=5 \Rightarrow (-x+1)+(3x-1)=5 \Rightarrow x=\frac{5}{2}$

For $x \geq 1$: $(x-1)+(3x-1)=5 \Rightarrow x=\frac{7}{4}$

The answer is $x=\frac{-3}{4}, \frac{7}{4}$.

My question: $x=\frac{5}{2}$ is not a solution because it is not in the domain of $\frac{1}{3} \leq x < 1$. So does this mean when $\frac{1}{3} \leq x < 1$, there is no solution to $|x-1|+|3x-1|=5$? If so, what does $x=\frac{5}{2}$ mean? How did this value come about? I guess I am saying if no solution exists, why am I able to compute a numerical value for $x$ despite it being wrong? Or to put it another way, by just using the definition of absolute value, this question is literally telling me when $\frac{1}{3} \leq x < 1$, $x=\frac{5}{2}$, a contradiction.

Answer 1

Perhaps this graph may help you understand. In each range, the function $|x-1|+|3x-1|$ is formed by a separate straight line. In two cases, the line intersects $y=5$ and so we have a solution. However, the middle red line does not intersect $y=5$, and so you are correct - there is no solution in this range. The value $x=\frac 52$ represents where the line would have intersected $y=5$, if it carried on outside of its range.

Answer 2

Good question. Let's look at something simpler: solve $x^2 = 4$ for $x > 10$.

There are two solutions to the first equation: $x = 2$ and $x = -2$. There are an infinite number of solutions to the second: $x = 10.32, x = 46, x = 13\pi, \ldots$, indeed, far too many to list in any way.

A solution to both equations must be in both of these sets, or to put it differently, it must be in the intersection of these two sets...but the intersection is empty. So there are no solutions to this pair of equations.

Now looking at your example, in the middle case you have a line, namely $2x = 5$, but are only looking for solutions in the range $\frac13 \le x < 1$. The solution set for the line-equation is $\{ \frac52\}$; the solution set for the "range specification" is all numbers between $\frac13$ and $1$, not including $1$ --- an infinite set. But the intersection of these two sets is empty, just as in my contrived example at the start.

Geometrically, the graph of $$ y = |x-1| + |3x - 1| - 5 $$ is made up of three line segments --- two of them infinite, the other a finite segment running between $x = 1/3$ and $x = 1$. What you've found -- $x = 5/2$ -- is where the middle line-segment would hit the $x$-axis if it were extended far enough. But that extension is not part of your graph, so it's not a solution to your problem.

Answer 3

"Or to put it another way, by just using the definition of absolute value, this question is literally telling me when $13\le x\lt1, x=\frac52$, a contradiction."

No. The absolute value branches the initial question into $3$ separate equations with each having certain constraints, imposed by the absolute value.

What it is telling you after you correctly finished with the algebra (i.e. solving these equations) is that a certain solution is discarded as contradicting one of the constraints. It's not some outside factor doing it but imposed by the absolute value itself.

Answer 4

Make a graph and see that $x=\frac 52$ fits in the interval $[1,\infty) \cap [\frac 13, \infty) = [1,\infty)$ and it is a valid solution.

Source: Geogebra