Is there a non-contractible simply-connected 4-manifold which is an Eilenberg-Mac Lane space?

Question

Let $M$ be a simply-connected non-contractible 4-manifold without boundary. Note that I am not assuming $M$ is closed.

Can it be the case that $M$ is a $K(G, n)$ for some abelian group $G$ and $n > 0$?

I suspect the answer is "no," but haven't been able to close out the case that $M$ is open. Here's what I've been able to come up with: First, note that the answer is "no" when $M$ is closed: Using Poincaré Duality, we immediately find that $H_1(M) = H^1(M) = H_3(M) = H^3(M) = 0$. If $H_2(M) = 0$ as well, then $M$ is a simply-connected integral homology sphere, thus homotopy equivalent to $S^4$ which is not an Eilenberg-Mac Lane space. Otherwise $H_2(M)$ must be finitely generated and torsion free (the torsion would appear as a summand of $H^3(M)$ which is trivial), so $H_2(M) \cong \mathbb{Z}^d$ for some $d > 0$. The only chance for $M$ to be an Eilenberg-Mac Lane space is thus if it is a $K(\mathbb{Z}^d, 2)$, but we know a model of this homotopy type, namely $(\mathbb{C}\mathrm{P}^\infty)^d$, which has non-trivial homology in infinitely many degrees, ruling out this possibility as well.

If $M$ is open, it can only be a $K(G, 2)$ or a $K(G, 3)$. In fact, it can only be a $K(G, 2)$: Any open 4-manifold has the homotopy type of a 3-dimensional CW-complex, so if it were a $K(G, 3)$ the group $G$ would have to be free of at most countable rank, and this is ruled out by the fact that $K(\mathbb{Z}, 3)$ has non-trivial homology in infinitely many degrees. The only thing I find myself able to say about the $K(G, 2)$-case is that $G$ cannot be finitely generated, for similar reasons. I haven't been able to rule out the case that $G$ is a non-finitely generated countable group, and don't feel like I have the necessary knowledge to do so (if my hunch that the statement is false is in fact correct). I know very little about 4-manifolds and definitely ought to brush up my knowledge of the theory of Eilenberg-Mac Lane spaces and their co/homology.

With these observations, my question thus becomes: Is there an open 4-manifold $M$ and a non-finitely generated countable group $G$ such that $M$ is a $K(G, 2)$?

---

Edit: I've managed to show that $G$ must be divisible. Indeed, note that $M$ must be a $M(G, 2)$ since $H_3(M)$ vanishes by Hurewicz and $H_k(M)$ vanishes for $k \geq 4$ since it is an open 4-manifold. Let $p \in \mathbb{N}$ be a prime number and consider the short exact sequence $$ 0 \to G \xrightarrow{\cdot p} G \to \underbrace{\operatorname{coker} (\cdot p)}_{=: G'} \to 0 $$ Applying $K({{-}}, 2)$ yields a fibre sequence $$ K(G, 2) \to K(G, 2) \to K(G', 2) $$ giving in turn rise to a Serre spectral sequence $$ E^2_{p, q} = H_p(K(G', 2); H_q(K(G, 2))) \implies H_{p + q}(K(G, 2)) $$ whose $E^2$-page looks like this: 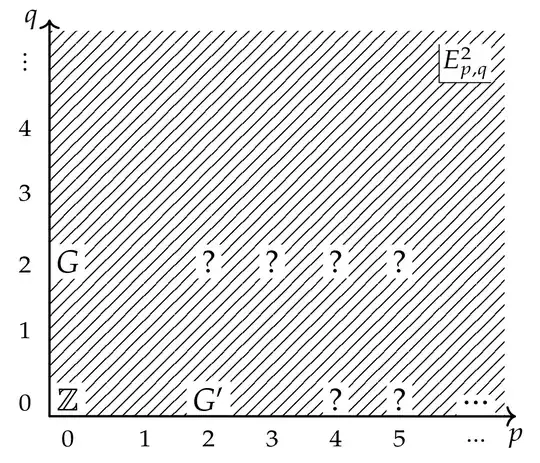(here everything shaded in is zero). Note that the group $E^2_{4, 0} = H_4(K(G', 2))$ is not affected by any differentials and survives to the $E^\infty$-page where it contributes to the convergence to $H_4(K(G, 2)) = 0$, so it suffices to show that this group is non-zero if $G'$ is for a contradiction. But note that $G'$ is an $\mathbb{F}_p$-vector space, so in fact it suffices to show that $H_4(K(\mathbb{Z} / p, 2)) \neq 0$, and this is easy: Simply note that $$ H^4(K(\mathbb{Z} / p, 2); \mathbb{Z} / p) \cong [K(\mathbb{Z} / p, 2), K(\mathbb{Z} / p, 4)] \neq 0 $$ since this latter set is in bijection with cohomology operations $H^2({{-}}; \mathbb{Z} / p) \Rightarrow H^4({{-}}; \mathbb{Z} / p)$ and the cup-square is one such operation, so since $H_3(K(\mathbb{Z} / p, 2)) = 0$ by Hurewicz the UCT implies that $H_4(K(\mathbb{Z} / p, 2)) \neq 0$. Letting $p$ range over all possible primes, we thus obtain that $G$ is divisible.

This implies that $G$ is a direct sum of copies of $\mathbb{Q}$ and of $\mathbb{Z}_{p^\infty}$ for prime $p$. In fact there are no summands of the first kind since $H^*(K(\mathbb{Q}, 2)) \cong \mathbb{Q}[\iota_2]$ is infinite-dimensional (see also this answer kindly linked by Moishe Kohan in the comments below). We can also rule out that there are copies of $\mathbb{Z}_{2^\infty}$, either by another spectral sequence argument analogous to the one above (consider $K(H, 2) \to K(G, 2) \to K(G, 2)$ where $H := \ker(G \xrightarrow{\cdot 2} G)$ and use that $H_4(K(\mathbb{Z} / 2, 2)) \cong \mathbb{Z} / 4$), or by virtue of this answer.

I have not been able to progress further. By the last answer I linked this answer is consistent at face value with the usual constraints being a manifold imposes on the co/homology (I have thought about Poincaré duality but found myself unable to say anything about $H^*_c(M)$ beyond what's implied by the duality theorem) and homotopy groups of $M$, and it seems unlikely that the tools I've used so far will carry me any further (unless there's a result on minimal cell structures of $K(\mathbb{Z}_{p^\infty}, 2)$s out there, but this strikes me as unlikely: These usually make use of co/homological dimension).

As I have stated above, I know very little about 4-manifolds, so I'm hoping that perhaps something can be said from that angle.

Summing up, the question thus reduces to: Is there an open 4-manifold $M$ which is a $K(G, 2)$ where $G$ is an at most countable sum of Prüfer groups $\mathbb{Z}_{p^\infty}$ for primes $p \neq 2$?

Of course answers using different routes of attack are also very welcome!

Answer 1

Suppose the four-manifold $M$ is a $K(G, 2)$ for $G$ non-trivial. Clearly $G$ is abelian and you've shown that $G$ must be divisible. Since $\pi_2$ of a four-manifold is always torsion-free (see below), $G$ must be a torsion-free divisible abelian group, and hence a vector space over $\mathbb{Q}$. As Moishe Kohan pointed out in the comments, this answer by André Henriques implies that $M$ would then have infinite cohomological dimension, contradicting the fact that $M$ is a four-manifold.

I did not come up with the proof of the following result, but I can't remember where I first saw it.

Proposition: If $M$ is a four-manifold, then $\pi_2(M)$ is torsion-free.

Proof: First, we can suppose that $M$ has no boundary (if it does, attach a collar neighbourhood to obtain a homotopy equivalent manifold without boundary). Passing to the universal cover, we can further reduce to the case that $M$ is simply connected.

By Hurewicz, we have $\pi_2(M) \cong H_2(M)$, and by Poincaré Duality, we have $H_2(M) \cong H^2_c(M)$. Recall that $H^2_c(M)$ is isomorphic to the direct limit $\varinjlim H^2(M, M\setminus K)$ over all compact subsets $K \subset M$. If a direct limit of groups has torsion, at least one of the groups has torsion, so it is enough to show that $H^2(M, M\setminus K)$ is always torsion-free.

Consider the long exact sequence in cohomology associated to the pair $(M, M\setminus K)$:

$$\dots \to H^1(M) \to H^1(M\setminus K) \to H^2(M, M\setminus K) \to H^2(M) \to \dots$$

By the Universal Coefficient Theorem

\begin{align*} H^1(M) &\cong \operatorname{Hom}(H_1(M), \mathbb{Z})\\ H^1(M\setminus K) &\cong \operatorname{Hom}(H_1(M\setminus K), \mathbb{Z})\\ H^2(M) &\cong \operatorname{Hom}(H_2(M), \mathbb{Z})\oplus\operatorname{Ext}(H_1(M), \mathbb{Z}) \end{align*}

Since $M$ is simply connected, $H_1(M) = 0$ so $H^1(M) = 0$ and $H^2(M) \cong \operatorname{Hom}(H_2(M), \mathbb{Z})$. As $\mathbb{Z}$ is torsion-free, it follows that $H^1(M\setminus K)$ and $H^2(M)$ are both torsion-free.

Finally, suppose $\alpha \in H^2(M, M\setminus K)$ is torsion. Since $H^2(M)$ is torsion-free, $\alpha$ lies in the kernel of the map $H^2(M, M\setminus K) \to H^2(M)$. By exactness, $\alpha$ therefore lies in the image of the map $H^1(M\setminus K) \to H^2(M, M\setminus K)$. As $H^1(M) = 0$, the map $H^1(M\setminus K) \to H^2(M, M\setminus K)$ is injective, so $\alpha$ is the image of a torsion element, but this is impossible as $H^1(M\setminus K)$ is torsion-free. Therefore $\alpha = 0$, i.e. $H^2(M, M\setminus K)$ is torsion-free. $\square$

Answer 2

This answer serves merely as an addendum to the accepted answer.

There is an error in the divisibility argument in the OP. Indeed, he assumes there is a short exact sequence $0\rightarrow G\stackrel{p\cdot}{\rightarrow}G\rightarrow G/pG\rightarrow0$, but this only makes sense if we already know $G$ to have no $p$-torsion. Thus, to obtain a correct argument, we have to first argue as in the accepted answer to obtain that $G$ is torsion-free and then we can conduct Ben's argument to obtain that $G$ is divisible. Together, this implies $G$ is a $\mathbb{Q}$-vector space, leading to a contradiction as has been explained in the OP.

Let me also present an alternative to the divisibility argument that is slightly more high-powered. There are isomorphisms $$H_{\bullet}(M;\mathbb{Q})\cong H_{\bullet}(K(G,2);\mathbb{Q})\cong H_{\bullet}(K(G\otimes\mathbb{Q},2);\mathbb{Q}).$$ For those familiar with rationalization, we are simply observing that $M_{\mathbb{Q}}\simeq K(G,2)_{\mathbb{Q}}\simeq K(G\otimes\mathbb{Q},2)$. That said, the isomorphism requires only part of the theory of localizations, namely the first two steps in the proof of the 'only if' part of Theorem 5.24,(b) in Allen Hatcher's Spectral Sequences. However, $G\otimes\mathbb{Q}$ is a $\mathbb{Q}$-vector space and $M$ has bounded homology, so we obtain as before that $G\otimes\mathbb{Q}=0$, i.e. $G$ is torsion. The argument in the accepted answer shows that $G$ torsion-free, so altogether $G=0$.

(The upshot of this alternative argument is that it generalizes to other even values of $n$. The argument in the accepted answer also generalizes to $\pi_{n-2}(M)$ for an $(n-3)$-connected $n$-manifold. Together, this yields that no $n$-manifold can be a $K(G,n-2)$ for $n\ge 2$ even.)