You begin with an m by n arrangement of prisoners arranged like a grid with a prisoner at each point where the gridlines cross. Each prisoner is evenly spaced with the one in front of him/her, behind him/her, to the left of him/her, and/or the right of him/her. Draw some squares. Think of the squares as prison walls They can be rotated and any size you like. The one constraint I'll have is that you cannot place the walls on top of the prisoners. The squares are allowed to overlap and share borders. What is the minimum amount of squares needed such that each prisoner is trapped in it's own region? We count the infinite outer region as "trapped". What I'm asking for is an explicit formula whose inputs are m and n (the amount and positioning of the prisoners) that outputs the minimum number of squares needed.
Here are some of the first few inputs and outputs of this function:
For a 1 by 1 arrangement of prisoners the answer is 0 (obviously).
For a 1 by 2 arrangement of prisoners the answer is 1.
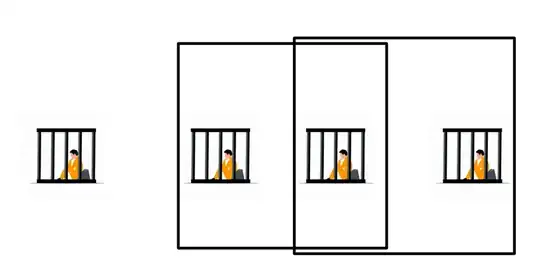
For a 1 by 3 arrangement of prisoners the answer is 2.
For a 1 by 4 arrangement of prisoners the answer is still 2.
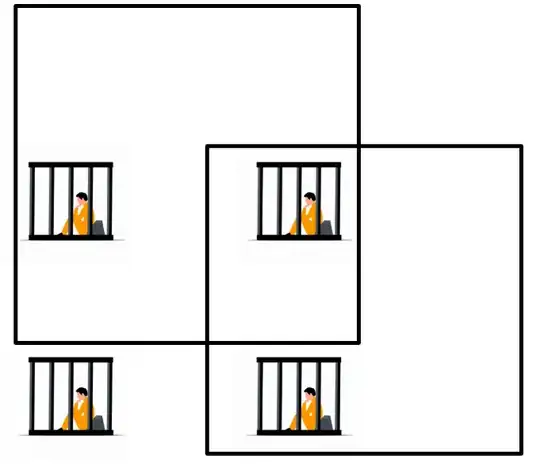
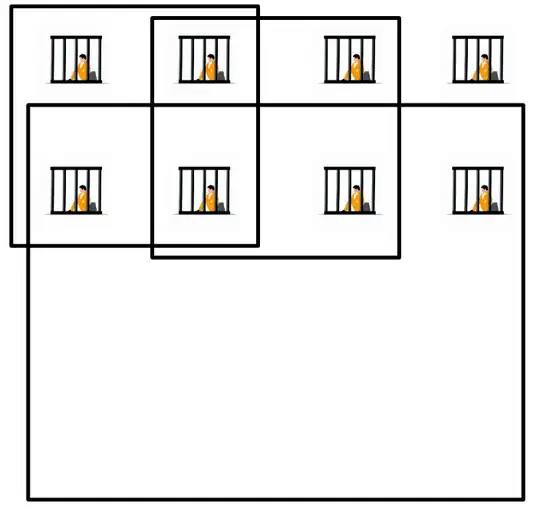
For a 2 by 2 arrangement of prisoners the answer is still 2.
For a 1 by 5 arrangement of prisoners the answer is now 3.
For a 1 by 6 arrangement of prisoners the answer is still 3.
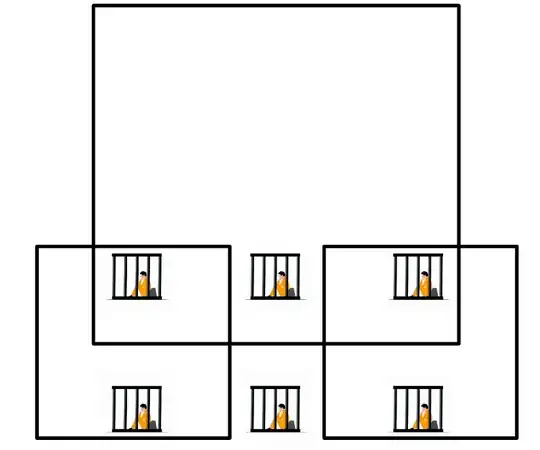
For a 2 by 3 arrangement of prisoners the answer is still 3.
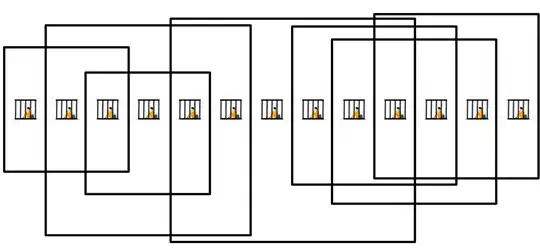
For a 1 by 7 arrangement of prisoners the answer is now 4.
For a 1 by 8 arrangement of prisoners the answer is still 4.
For a 2 by 4 arrangement of prisoners the answer has gone back down to 3.
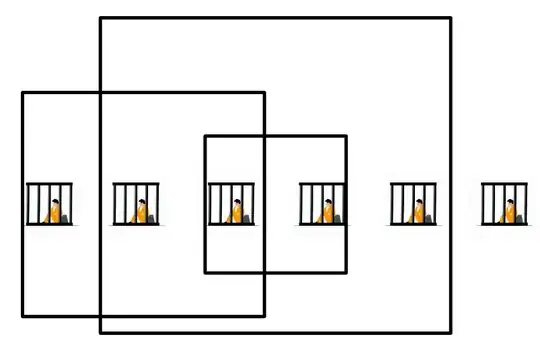
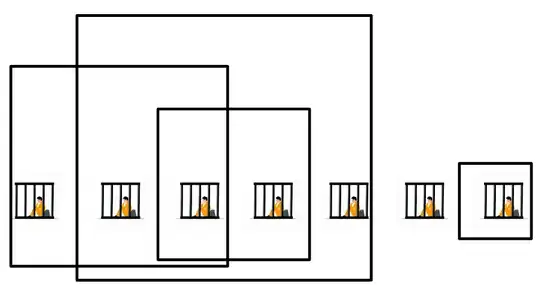
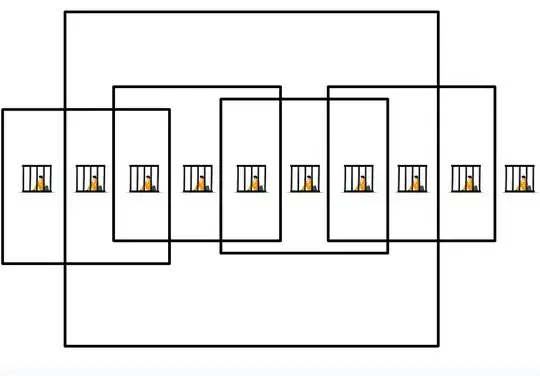
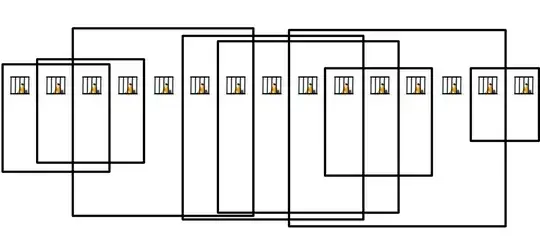
For a 1 by 9 arrangement of prisoners the answer is now 5.
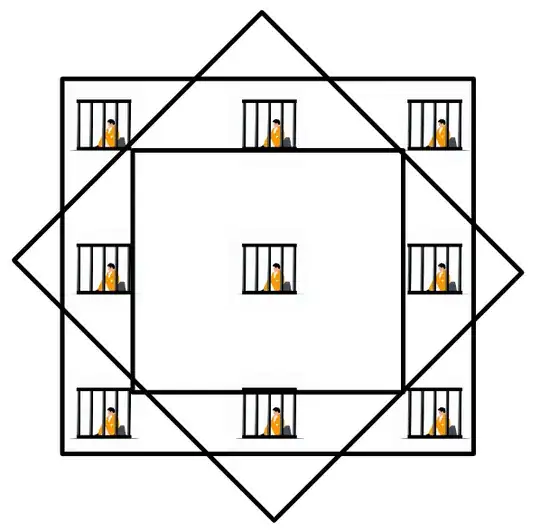
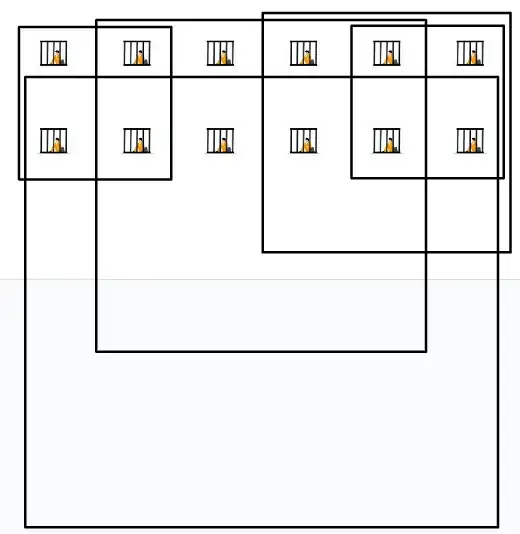
For a 3 by 3 arrangement of prisoners the answer has returned to 3 (I personally find this one to be the most visually pleasing).
For a 1 by 10 arrangement of prisoners the answer is 5 again.
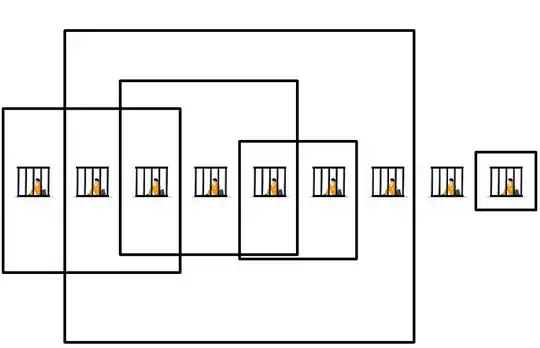
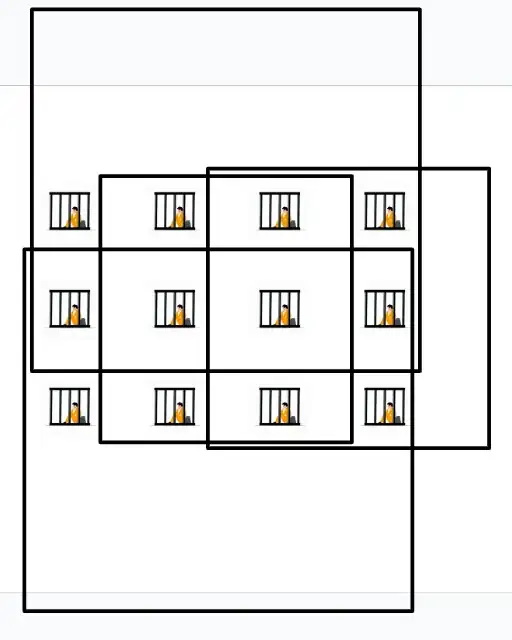
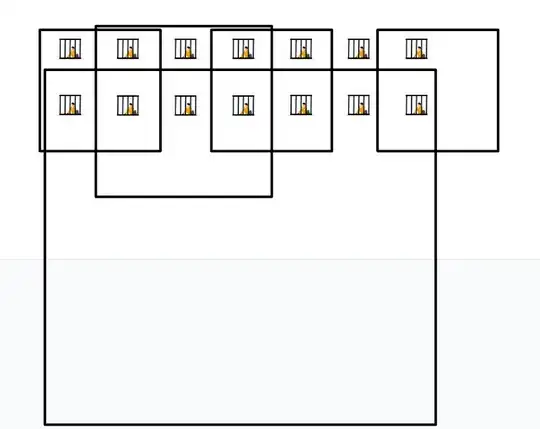
For a 2 by 5 arrangement of prisoners the answer is 4 (ignore the gray horizontal lines at the top and bottom of this picture).
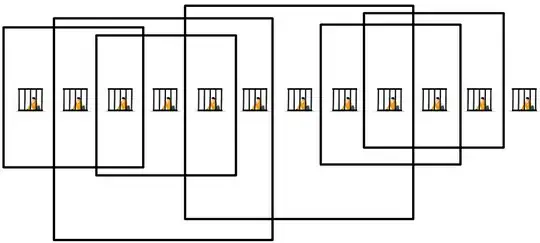
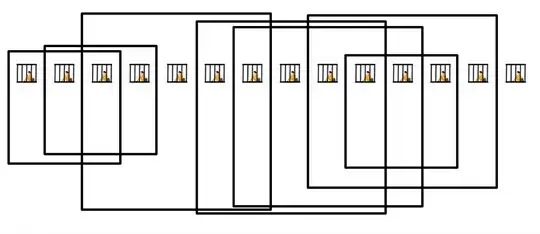
For a 1 by 11 arrangement of prisoners the answer is 6.
For a 1 by 12 arrangement of prisoners the answer is still 6.
For a 2 by 6 arrangement of prisoners the answer is back to 5.
For a 3 by 4 arrangement of prisoners the answer has dropped to 4.
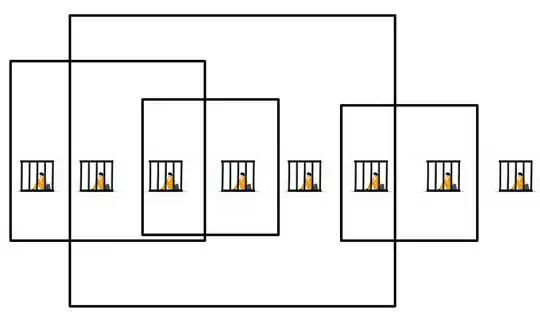
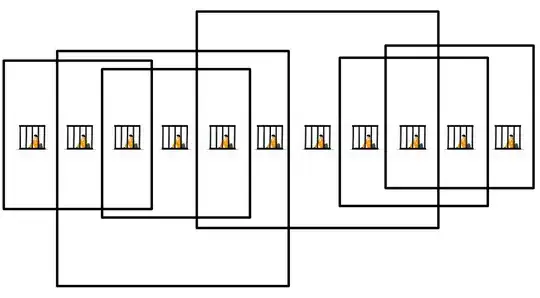
For a 1 by 13 arrangement of prisoners the answer has jumped to 7.
For a 1 by 14 arrangement of prisoners the answer is still 7.
For a 2 by 7 arrangement of prisoners the answer is down to 5.
For a 1 by 15 arrangement of prisoners the answer has jumped to 8.
For a 3 by 5 arrangement of prisoners the answer is back to 5.
If you look closely you may notice that these aren't squares but rectangles. Ignore that. They are supposed to be squares. Please let me know if you find more efficient solutions to any of these.
An observation I made is that for a 1 by n grid or prisoners, the answer always seems to be ceil(n/2) (with the exception of 1 prisoner). Another observation I have made is that when you increase m or n by 1, the answer increases by 0 or 1, never by 2 or more.
My current proven upper bound is $mn-1$ (I know this is kind of obvious). I currently have no lower bound. Please let me know if you are able to prove better upper or lower bounds.
(I put Geometry and Euclidean-geometry under the tags section because I have no idea what branch of math this falls into. Let me know if you know of a better fitting tag.)