2

I'm reading Greenberg's "Algebraic Topology" and I have the next proposition:
Proposition A contractible space is simply connected.

Now, to prove this, author use the following lemma:

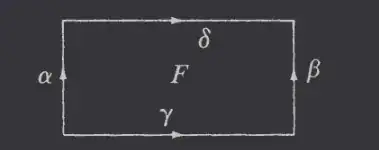
Lemma Given $F:I \times I \to X$, set $\alpha(t) = F(0,t),\, \beta(t) = F(1,t),\, \gamma(s) = F(s,0),\, \delta(s) = F(s,1)$, so diagrammatically we have this:

enter image description here

Then, $\delta \sim \alpha^{-1} \gamma \beta$ rel $(0,1)$.

Now, he prove the proposition: Although every loop $\sigma$ at a point $x_0$ is homotopic as a map with the constant loop, we do not know if they are homotopic relative to $(0,1)$.

Now, we use lemma. Because $X$ is contractible, we can obtain such an $F$ with $\delta = \sigma, \gamma = x_0$ and $\alpha = \beta$ (since $\sigma$ induces a map of the circle into $X$ which is homotopic to the constant map at $x_0$), hence $\sigma$ is homotopically trivial.

I don't understand how we can obtain such an $F$ with $\alpha = \beta$ and how this map of $S^1$ into $X$ help... And also I know simply connected spaces are path-connected and this is not proved by the author. This result from some fact in the proof?
Moishe Kohan
  • 111,854
ProofSeeker
  • 1,396

1 Answers1

3

You need Exercise (3.1):

$X$ is contractible if and only if for any space $Y$ any two maps of $Y$ into $X$ are homotopic. A contractible space is pathwise connected.

This is easy to prove:

Let $f, g : Y \to X$ be two maps and $H : X \times I \to $ be a homotopy from $id_X$ to a constant map $c : X \to X$ (with value $x_0 \in X$). Then $f = id_X \circ f \simeq c \circ f = c \circ g \simeq id_X \circ g = g$. Taking for $Y$ a one-point space yields pathwise connectedness.

To prove that contractible implies simply connected, it therefore suffices to show that each loop $\sigma$ based at a point $x_0 \in X$ is homotopic to the constant loop rel. $(0,1)$.

In my opinion Greenberg's proof is a bit short. He uses the fact that loops $u : I \to X$ based at $x_0$ can be identified with maps $\bar u : S^1 = \{z \in \mathbb C \mid \lvert z \rvert = 1\} \to X$ with $\bar u(1) = x_0$ and homotopies $H : I \times I \to X$ between loops $u,v$ based at $x_0$ which are homotopies rel. $(0,1)$ can be identified with homotopies $\bar H : S^1 \times I \to X$ from $\bar u$ to $\bar v$ with the property $H(1,t) = x_0$ for all $t \in I$. See Characterizing simply connected spaces for details.

However, we do not need that (nor do we really need Lemma (3.3)). Define a map $\Sigma$ from the boundary $B = I \times \{0,1\} \cup \{0,1\} \times I$ of $I \times I$ to $X$ by $\Sigma(s,0) = \sigma(s)$,$\Sigma(s,1) = x_0$ and $\Sigma(0,t) = \Sigma(1,t) = x_0$. This map is homotopic to the constant map $C : B \to X$ with value $x_0$ via a homotopy $G$. It is easy to see that there is a quotient map $q :B \times I \to I \times I$ such that $q(b,0) = b$ for $b \in B$ which maps $B \times [0,1)$ homeomorphically onto $I \times I \setminus \{(\frac 1 2, \frac 1 2)\}$ and identifies $B \times \{1\}$ to $(\frac 1 2, \frac 1 2)$: Simply map each $\{b\} \times I$ linearly to the line segment in $I \times I$ connecting $b$ with $(\frac 1 2, \frac 1 2)$. An explicit formula is easily obtained.

By the above properties of $q$ there exists a unique function $H : I \times I \to X$ such that $H \circ q = G$. By the universal property of the quotient topology this function is continuous. Due to the construction $H$ is an extension of $\Sigma$ and therefore a homotopy rel. $(0,1)$ from $\sigma$ to the constant loop.

Paul Frost
  • 87,968