2

This equation $2 x^2 - 2 x^3 - 6 y + 7 x y + x^2 y - 4 y^2=0$ came up while investigating some quartic curve, under a substitution. Managed to get some rational points $(0,0)$, $(0,-3/2)$, $(1,0)$, $(1,1/2)$,$(2,1)$, $(2,2)$, $(3,3)$. The usual methods ( secants through two points, tangents through a point) do not seem to produce more points ( or I am just doing something wrong).

I would appreciate somebody to explain some general methods to get the group of rational points. I just know very little about elliptic curves. Thanks for your interest!

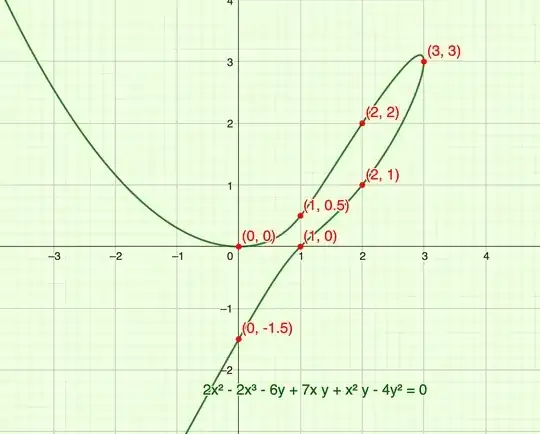
eliptic curve

orangeskid
  • 56,630
  • 3
    You might be interested in this https://math.stackexchange.com/questions/203484/how-to-compute-rational-or-integer-points-on-elliptic-curves?rq=1 – rafilou2003 Jan 08 '25 at 00:23

1 Answers1

5

We have the curve $$4y^2-x^2y-7xy+6y=2x^2-2x^3.$$ To keep only a squared term on the LHS, perform the substitution $$y=m+\frac{x^2+7x-6}{8}$$ and multiply by $16$ on both sides to obtain $$\left(8m\right)^2=x^4-18x^3+69x^2-84x+36=\left(x-3\right)\left(x^3-15x^2+24x-12\right).$$ We now perform the substitution $$x=3+\frac{1}{t}$$ to send the branch point $x=3$ to infinity and multiply both sides by $t^4$ to obtain the Weierstrass model $$\left(8t^2m\right)^2=-48t^3-39t^2-6t+1.$$ Now taking $t=-3s$ and dividing by $36^2$ gives $$\left(2s^2m\right)^2=s^3-\frac{13}{48}s^2+\frac{1}{72}s+\frac{1}{1296}.$$ Now writing $s=X+\frac{13}{3\cdot 48}$ and $Y=2s^2 m$ finally gives the elliptic curve $$E: \qquad Y^2=X^3-\frac{73}{6912}X+\frac{827}{1492992}.$$ Now since all of our substitutions to this point have been rational functions, any rational point on our original curve will correspond to a rational point on this elliptic curve and vice versa (except in the case that a rational point gets sent to infinity as we shall see).

Inputting the elliptic curve $E$ into sage, we find that it is an elliptic curve of conductor $54$ and rank $0$, meaning any rational points on $E$ must be a torsion point. Sage gives us that $E(\mathbb{Q})_{\mathrm{tors}}\cong\mathbb{Z}/9\mathbb{Z}$ and listing the elements (excluding the point at infinity): $$(X,Y)=\left(\frac{11}{144},\pm\frac{1}{72}\right),\left(-\frac{13}{144},\pm\frac{1}{36}\right),\left(\frac{1}{48},\pm\frac{1}{54}\right),\left(\frac{35}{144},-\frac{1}{9}\right).$$ The points $\left(-\frac{13}{144},\pm\frac{1}{36}\right)$ get sent to infinity by our inversion substitution in $t$, so they are extraneous solutions and are discarded. The solution at infinity gets sent to the point $(3,3)$. Thus upon unfurling the equations, we recover all $7$ rational points you found on your original curve, and there are no others.

KStar
  • 6,211
  • Wow, thank you, this is very informative! Surprising how the standard form has fairly involved coefficients. – orangeskid Jan 08 '25 at 04:17
  • 1
    Indeed. I should have probably elaborated on why the point addition operation wasn’t yielding any new rational points: these points cycle around and have finite orders and are why we call them torsion points. You cannot generate any other rational points from these once you have them all. The curve has rank $0$ so only has finitely (see Mazur’s theorem for a more precise classification on the possible order of the group of torsion points) many rational points, namely the torsion points. If the rank were $>0$, then we could find a Mordell-Weil point to generate infinitely many rational points. – KStar Jan 08 '25 at 04:36
  • 1
    @orangeskid In case you may be wondering about how one proves the rank is indeed $0$, by Kolyvagin’s theorem it suffices to show $L(E,1)\neq 0$. One can compute some terms of the associated $L$-function at $s=1$ and compute certain bounds to determine an error from the true value. Once this error is smaller than $L(E,1)$, you can be confident that $L(E,1)\neq 0$. In fact, for what it is worth, for rank $0$ elliptic curves, we can give $L(E,1)$ exactly in terms of the complete elliptic integral of the first kind and the three roots of the cubic in $x$. – KStar Jan 08 '25 at 04:46
  • 2
    In terms of algorithmically finding rational points on a given elliptic curve, this is often hard and sometimes sage computations can go on for several days for most curves. The general idea is doing search and employing Nagell-Lutz for torsion points, and things like $2$-descent to bound the rank. Once you have a torsion point, you can repeatedly do point addition on itself to at least obtain a subgroup of the torsion points. Height pairings are used to try to find generator points if the rank is greater than $0$. – KStar Jan 08 '25 at 04:58
  • 3
    The less "heavy-machinery" way to prove that $E$ has rank 0 would be a descent by $3$-isogeny (leveraging the $\mathbb{Z}/3\mathbb{Z}$ subgroup, giving a rational $3$-isogeny). Or, in these days you can just enter the Weierstrass equation into LMFDB to find the curve. – pzq_alex Jan 08 '25 at 11:42
  • Amazing comments too, should brush up on the material – orangeskid Jan 08 '25 at 16:40
  • just noticed that there are two points at infinity, $(0:1:0)$ and $(1:2:0)$, so we get in total $9$ rational points, a bit clearer now :-) – orangeskid Jan 09 '25 at 02:57
  • @pzq_alex: Thank you, very informative! So, are you saying that the link has the minimal model of the curve? ( will have to study that) – orangeskid Jan 09 '25 at 03:21
  • @orangeskid Yes. – pzq_alex Jan 09 '25 at 09:55