What is the (geometric) intuition of the matrix transpose?

Question

There are a lot of discussions on the matrix transpose already, but none of them seem to give a satisfying (visual) intuition. I guess I have collected the most, if not even all, ways to view and understand the transpose of a matrix.

My knowledge so far behind the transpose of a matrix

Algebraic perspective

Switching rows & columns

Connection to dual vectors & spaces

The rows of a matrix $A$ act on (contravariant) vectors, while the columns of a matrix act on covariant vectors / dual vectors / linear functionals. The transpose represents the linear transformation of the dual space to preserve the relation between contravariant and covariant vectors.

Here I personally like the answer of Manu in What is the geometric interpretation of the transpose? since it gives a illustrative simple example.

Switching the column- & row space of a linear transformation

If $A \in \mathbb R^{m \times n}$ is a linear transformation mapping from the row space / domain to the column space / image of the linear transformation, then is the transpose $A^T \in \mathbb R^{n \times m}$ does the opposite.

Preserving the dot product

Applying a matrix $A$ to a vector is the same as applying its transpose $A^T$ to the other vector in the dot product like $\langle A \underline x, \underline y \rangle = \langle \underline x, A^T \underline y \rangle$ as already answered by Berci in What's the intuition of the transpose of a matrix? [duplicate].

Singular value decomposition (SVD)

Every matrix can be described by three actions described by $A = U \Lambda V^T$ and $A^T = V \Lambda^T U^T$ where $\Lambda$ simply scales the vector and $U$ & $V$ are rotations. This was also described well by Chris Taylor in What is the geometric interpretation of the transpose?

Product of a matrix with its transpose

The product $A^T A$ and $A A^T$ are always square and symmetric. This is also linked to the Singular value decompostion.

Questions

• 1. What does happen to $\underline x$ geometrically in $A^T \underline x$?
• 2. What does it look like to map the image / column space $Col(A)$ back to the domain / row space $Row(A)$?
• 3. How does this transformation $A^T \underline x$ compare geometrically to $A^{-1}x$?
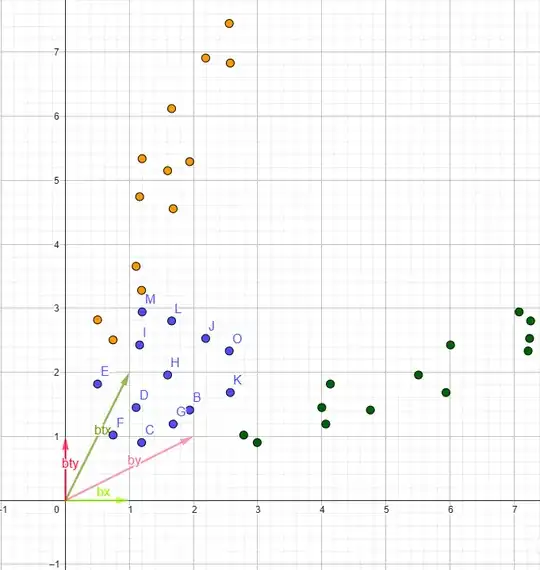
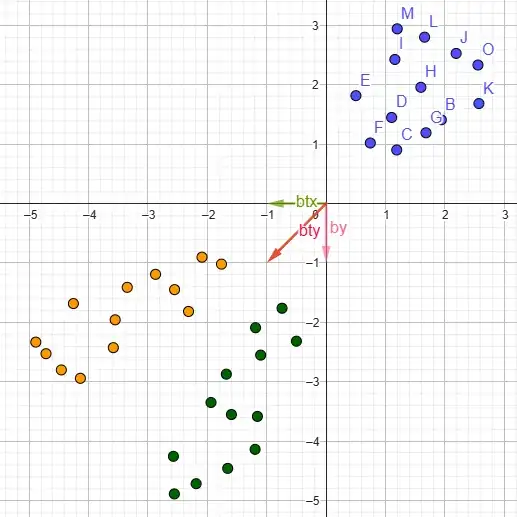
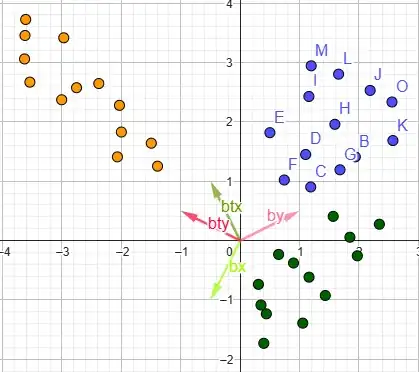
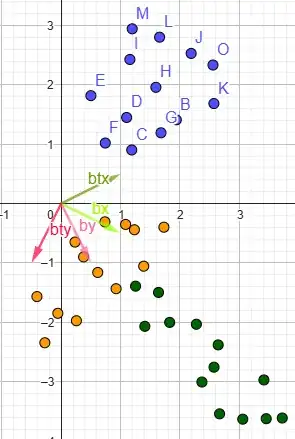
• 4. Why does $A^T$ simply mirror the basis vectors along $y=x$ in the 1st & 3rd quadrant, while in the 2nd & 4th quadrant it seems to get stretched in the opposite direction of $A$ along $y=-x$? See images below

Regarding the images - from top to bottom they use these matrices:

$A_1 = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix}$ $A_2 = \begin{bmatrix} -1 & -1 \\ 0 & -1 \end{bmatrix}$ $A_3 = \begin{bmatrix} -0.5 & 1 \\ -1 & 0.5 \end{bmatrix}$ $A_4 = \begin{bmatrix} 1 & -0.5 \\ 0.5 & -1 \end{bmatrix}$ $A_5 = \begin{bmatrix} 1 & -1 \\ 0 & 1 \end{bmatrix}$

Additionally there are the basis vectors $\underline b_x$ & $\underline b_y$ of the $A$ matrix and the basis vectors of the transpose $\underline b_{tx}$ & $\underline b_{ty}$ of the $A^T$ matrix. The green dots are the fixed blue dots transformed by $A$, while the yellow dots are the fixed blue dots transformed by $A^T$.