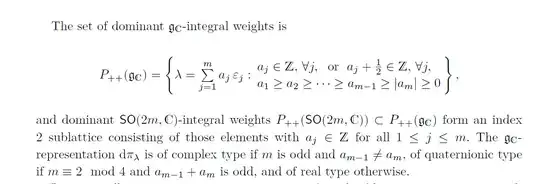A question about SO(2m,C)-represention

Question

I am reading a thesis about geometry and representation theory. it gives a example about $so(2m,c)$. it gives fundamental weight and dominant $g_C$-integral weights. For any element of dominant $g_C$-integral weights $\lambda$, we can find a representation $d\pi_\lambda$ with highest weight $\lambda$ by highest weight theorem. The representation is judged by the highest weight element $\lambda$ to be real type, complex type, or quaternion type. I want to know how to prove the relationship between dominant $g_C$-integral weights and representation classification. Or which book has the relevant knowledge on the subject？

The following is the original text

Answer 1

You can look at Chapter 26.3 of Fulton and Harris, which gives an overview for classifying the types of representations of classical semisimple Lie algebras. Otherwise, here is a general summary regarding your question on how to classify the types of highest weight representations of a semisimple Lie algebra $\mathfrak{g}$.

First, you can classify all complex highest weight representations by determining those that are not self-dual. In general, if $\lambda$ is a dominant weight, then the dual of $d\pi_{\lambda}$ is a module of highest weight $-w_0(\lambda)$ where $w_0$ is the longest element of the Weyl group of $\mathfrak{g}$ (see Ch. VI in Lie Groups and Algebras by Bourbaki). So, $d\pi_{\lambda}$ is complex if and only if $-w_0(\lambda) \neq \lambda$.

Example. Let $\mathfrak{g} = \mathfrak{sl}_n(\mathbb{C})$ and let $e_k$ for $1 \leq k \leq n - 1$ be the fundamental weights. If $\lambda = \sum_{k = 1}^{n-1} a_k e_k$, then $-w_0(\lambda) = \sum_{k = 1}^{n-1} a_k e_{n-k}$ i.e. $-w_0$ "reverses" the components of $\lambda$. So, $d\pi_{\lambda}$ is complex if and only if there exists $1 \leq k \leq (n-1)/2$ such that $a_k \neq a_{n-k}$.

Example. Let $\mathfrak{g} = \mathfrak{so}_{2m}(\mathbb{C})$ and let $e_k$ for $1 \leq k \leq m$ be the fundamental weights where $e_{m-1}$ and $e_{m}$ correspond to the two half-spin representations. Let $\lambda = \sum_{k = 1}^{n-1} a_k e_k$. If $m$ is even, then $-w_0(\lambda) = \lambda$. If $m$ is odd, then $-w_0$ swaps the $e_{m}$ and $e_{m-1}$ components and fixes all other components. So, if $m$ is even, then every $\mathfrak{so}_{2m}(\mathbb{C})$ representation is real or quaternionic. If $m$ is odd, then $d\pi_{\lambda}$ is complex if and only if $a_{m} \neq a_{m-1}$.

Regarding $w_0$ for other cases of $\mathfrak{g}$, see this answer.

Now, we want a way to determine if a self-dual highest weight representation is real or quaternionic. First, we determine the types of the representations corresponding to fundamental weight (through some direct investigation), then the following lemma gives the type of all highest weight representations.

Lemma (Exercise from Fulton and Harris). Let $\lambda$ and $\mu$ be dominant weights. We have the following:

1. If $d\pi_{\lambda}$ and $d\pi_{\mu}$ are both real or both quaternionic, then $d\pi_{\lambda + \mu}$ is real.
2. If $d\pi_{\lambda}$ is real and $d\pi_{\mu}$ is quaternionic, then $d\pi_{\lambda + \mu}$ is quaternionic.
3. If $d\pi_{\lambda}$ and $d\pi_{\mu}$, are complex and dual then $d\pi_{\lambda + \mu}$ is real.

Given a dominant weight $\lambda$ which corresponds to a non-complex representation, consider the sum of the components corresponding to quaternionic fundamental weights. By the lemma, this sum is even if and only if $\lambda$ is real (and odd if and only if $\lambda$ is quaternionic).

Example. Let $\mathfrak{g} = \mathfrak{so}_{2m}(\mathbb{C})$ and define $e_k$ as before. We have the following cases for different $m$:

1. If $m = 1$, then $e_1$ is quaternionic ($\mathfrak{g} \cong \mathfrak{sl}_{2}(\mathbb{C})$) so $\lambda = a_1 e_1$ is quaternionic if $a_1$ is odd and real otherwise.
2. If $m = 2$, then $e_1$ and $e_2$ are quaternionic ($\mathfrak{g} \cong \mathfrak{sl}_{2}(\mathbb{C})^2$) so $\lambda = a_1 e_1 + a_2 e_2$ is quaternionic if $a_1 + a_2$ is odd and real otherwise.
3. For any $m \geq 3$, $e_1,\ldots,e_{m-2}$ are all real. The types of $e_{m-1}$ and $e_{m-2}$ depend on $m$ mod 4.
   1. If $m$ is odd, then $e_{m-1}$ and $e_m$ are dual (so both complex). Thus, $\lambda = \sum_{k = 1}^{m} a_k e_k$ is real if $a_{m-1} = a_m$ and complex otherwise.
   2. If $m$ is congruent to $2$ mod $4$, then $e_m$ and $e_{m-1}$ are quaternionic. Thus, $\lambda = \sum_{k = 1}^{m} a_k e_k$ is real if and only if $a_{m-1} + a_m$ is even.
   3. If $m$ is congruent to $0$ mod $4$, then $e_m$ and $e_{m-1}$ are real. Thus, any representation is real.