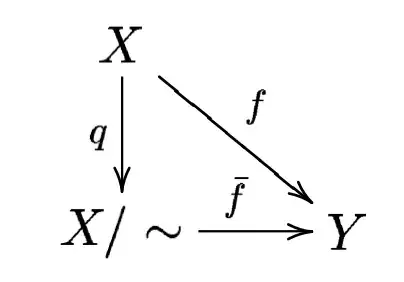I was trying to prove that the image of a (closed) plane Jordan curve is homeomorphic to $S^1$ and it looks like I managed to prove a much stronger result, so I would like to know if my proof is correct.
I have been given the following definitions (I will always assume $C^\infty$):
A parametrized curve in $\mathbb{R^n}$ is a function $\sigma:I\subseteq \mathbb{R} \to \mathbb{R^n}.$
Two parametrized curves $\sigma:I\to \mathbb{R^n}, \hat\sigma:\hat I\to \mathbb{R^n}$ are equivalent if there is a diffeomorphism $h: \hat I\to I$ such that $\hat\sigma=\sigma \circ h.$ We say that $\hat\sigma$ is a reparametrization of $\sigma.$
A curve is an equivalence class of parametrized curves.
Finally:
A Jordan curve in $\mathbb{R^n}$ is a curve C with a parametrization $\sigma:[a,b]\to \mathbb{R^n}$ which is closed, i.e. $\sigma(a)=\sigma(b)$, and injective on $[a,b)$ and $(a,b].$
We can assume $[a,b]=[0,1]$ via reparametrization. First of all I will define an equivalence relation on $[0,1]$. Let $x\sim y \iff x=y \vee (x,y)=(0,1) \vee (x,y)=(1,0)$. Then, by "glueing" $0$ and $1$, $S^1$ and $[0,1]/\sim$ are clearly homeomorphic. I will recall the proof of this fact as it will be helpful later; unfortunately, I read it is very difficult to draw a triangular commutative diagram here, so I must use a picture. Take $X=[0,1]$, $q$ the projection, $Y=S^1$ and $f(t)=e^{2\pi it}.$
It is known from topology that whenever $f$ is continuous and constant on the equivalence classes, also $\bar f$ is continuous. In this case these two hypotheses hold, so $\bar f$ is continuous; $\bar f$ is also a bijection (it is easy to verify that it is both injective and surjective); lastly $\bar f$ is closed since it is a map from the compact space $[0,1]/\sim$ to the Hausdorff space $S^1$
Now take $Y=Im(C)$ and $f(t)=\sigma(t).$ Since $\sigma(0)=\sigma(1)$, we can proceed like before. Therefore $Im(C)$ is also homeomorphic to $[0,1]/\sim$ and by transitivity it is homeomorphic to $S^1$.
Reasons for asking: I am not sure about the part where I say "we can proceed like before". This proof looks too easy and I only used the continuity of $\sigma$, while it is actually $C^\infty$. Here I read that the image of a continuous map is homeomorphic to $S^1$, and this makes me feel a bit relieved. However, it looks like I didn't even use the fact that $C$ is a plane curve! I also find it weird that I couldn't find this proof online. The main topic of my post was addressed here, but with a different approach. Moreover, in both the previous posts, users talk about plane simple curves, which makes me think something is wrong with my proof.
Credits: I recalled some topology facts mentioned here; I have found the diagram there too.
Feel free to edit the tags :)