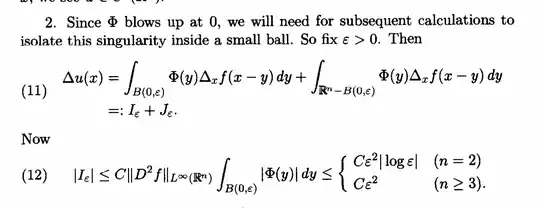Poisson's equation in Evan's PDES

Question

I am quite confused as to the following theorem and proof from Evan's PDE

where $$\Phi(x) = \begin{cases} - \frac{1}{2 \pi} \log |x| & \text{if $n= 2$} \\ \frac{1}{n(n-2)\alpha (n)} \frac{1}{|x|^{n-2}} &\text{if $n \geq 3$} \end{cases},$$

My issue with the proof is that I do not see how you can't justify $u$ being twice differentiable. I found a stackexchange post asking this very same question

theorem 1 chapter 2 - Evans PDE

Some of the people asking the post said that $\Phi$ is locally integrable, however, I do not agree. When $n=3$, along any ball centered about the origin we do not have integrability. Someone seemed to have a similar concern as mine in this post:evans book pde estimate question, however, the accepted answer seems to suggest that we "just" need to use polar coordinates. The theorem they quote in the appendix of Evans book seems to require continuity, and this is is not present here.

Could someone help me understand what is going on here?

Question: I do not see how what is given proves that $u$ is twice differentiable. The author claims it is by uniform continuity, then there is a stack exchange post elaborating on it. The logic of the post seems faulty since Φ is not locally integrable when =3 . My question is, am I right in thinking that Φ is not locally integrable, and if so, how does one approach proving the theorem then?

Answer 1

First of all, $\Phi$ IS locally integrable, even if though you can’t use the exact version of the theorem Evans quotes in the appendix. Actually, continuity on all of $\Bbb{R}^n$ is NOT essential to that theorem; the same conclusion holds even if you’re continuous away from the origin. In fact notice that Evans doesn’t prove either of the theorems in the appendices related to the coarea formula, instead he relegates them to his other reference: Evans, Gariepy, Measure Theory and Fine Properties of Functions, in particular there’s a very strong version of the coarea and change of variables formulae.

You just need this ‘vanilla’ version of the change of variables formulae, and know that the spherical coordinate parametrization covers $\Bbb{R}^n$ minus a set of $n$-dimensional Lebesgue measure-zero. As a corollary of that, we immediately deduce the following:

Lemma: Radial Integrals

Let $f:\Bbb{R}^n\to [0,\infty]$ be a Borel-measurable radial function, meaning there exists a (necessarily measurable) function $\phi:(0,\infty)\to [0,\infty]$ such that for all $x\in\Bbb{R}^n\setminus\{0\}$, we have $f(x)=\phi(\|x\|)$. Then, \begin{align} \int_{\Bbb{R}^n}f(x)\,dx&=\int_0^{\infty}\phi(r)\cdot A_{n-1}r^{n-1}\,dr. \end{align} Here, $A_{n-1}$ is the surface area of the unit sphere $S^{n-1}\subset\Bbb{R}^n$ (which happens to equal $\frac{2\pi^{n/2}}{\Gamma(n/2)}$, which equals $4\pi$ when $n=3$).

Notice carefully that we do not need continuity of $f$. I have several other answers about the change of variables theorem in various levels of generality (manifolds or not) several of which are linked in the comments to this question.

Anyway, with the lemma above, we can easily apply it to $f(x)=\mathbf{1}_{B_{1}(0)}(x)\cdot \frac{1}{\|x\|^{p}}$ and you see that \begin{align} \int_{B_R(0)}\frac{1}{\|x\|^p}\,dx&=\int_0^R\frac{1}{r^p}\cdot A_{n-1}r^{n-1}\,dr=A_{n-1}\int_0^{R}\frac{1}{r^{p-n+1}}\,dr, \end{align} and by first year calculus the latter is finite if and only if $p-n+1<1$, i.e if and only if $p<n$.

Thus, for all $n\geq 3$, the function $\Phi$ is indeed integrable on every bounded ball around the origin (and hence is locally integrable). For $n=2$, a similar story: \begin{align} \int_{B_R(0)}|\Phi(x)|\,dx&=\frac{1}{2\pi}\int_0^R|\log r|\cdot 2\pi r\,dr, \end{align} and this is finite since $r\mapsto r\log r$ extends continuously to $[0,\infty)$ (the limit as $r\to 0^+$ is $0$).