Triple integral in spherical coordinates over a tetrahedron

Question

Happy New Year!

I am trying to evaluate a triple integral where the domain $T$ is the tetrahedron with its vertices at $(0, 0, 0)$, $(2, 0, 0)$, $(2, 2, 0)$, and $(2, 0, 2)$.

I am trying to express the integral as repeated integrals using spherical coordinates.

My problem is: does $\rho$ go from $0$ to the surface $x=2$, $\phi$ from $\frac\pi4$ to $\frac\pi2$, and $\theta$ from $0$ to $\frac\pi4$?

Thanks for any help.

Answer 1

Does $\rho$ go from $0$ to the surface $x=2$, $\phi$ from $\dfrac\pi4$ to $\dfrac\pi2$, and $\theta$ from $0$ to $\dfrac\pi4$ ?

We can lock in these ranges for $\rho$ and $\phi$, but we need to be more careful with $\theta$ due to the dependency between $\theta$ and $\phi$:

$$z=x-y \implies (\cos\theta - \sin\theta)\tan\phi=1 \implies \cot\phi=\sqrt2\sin\left(\frac\pi4-\theta\right)$$

Take a radial cross section of $T$ in the half-plane $\theta=0$, i.e. the face of $T$ in the plane $y=0$. On this face, the cross section is a right triangle with hypotenuse $2\sqrt2$, and so the lower limit for the polar angle $\phi$ would indeed be $\dfrac\pi4$.

Now take another section at, say, $\theta=\dfrac\pi8$, lying in the plane $y=\left(\tan\dfrac\pi8\right)x=\left(\sqrt2-1\right)x$. The right triangle's hypotenuse is shortened and the lowest $\phi$ can go is now $\operatorname{arccot}\left(\sqrt2\sin\dfrac\pi8\right)=\arctan\sqrt{2+\sqrt2}>\dfrac\pi4$.

$T$" />

Based on this breakdown of $T$, one way to set up the integral (assuming an integrand of $1$) would be

$$\int_0^\tfrac\pi4 \int_{\operatorname{arccot}\left(\sqrt2\sin\left(\tfrac\pi4-\theta\right)\right)}^\tfrac\pi2 \int_0^{2\sec\theta\csc\phi} \rho^2\sin\phi\,d\rho\,d\phi\,d\theta$$

A similar analysis by taking sections of $T$ in various half-planes corresponding to fixed $\phi$ yields the target integral,

$$\int_\tfrac\pi4^\tfrac\pi2 \int_0^{\tfrac\pi4-\operatorname{arccsc}\left(\sqrt2\tan\phi\right)} \int_0^{2\sec\theta\csc\phi} \rho^2 \sin\phi \, d\rho\,d\theta\,d\phi$$

Answer 2

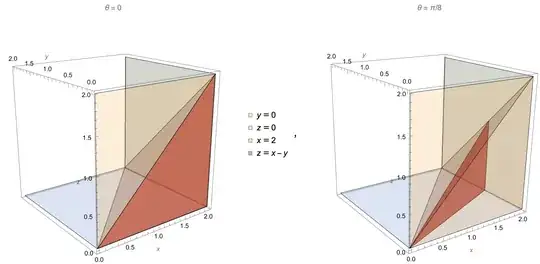
The region condition is

     RegionConvert[ 
         Simplex[{{0, 0, 0}, {2, 0, 0}, {2, 2, 0}, {2, 0, 2}}],
         "Implicit"]
      ImplicitRegion[x >= y + z && y >= 0 && z >= 0 && 
       x <= 2, {x, y, z}]

$$0\leq z\leq 2\land ((0\leq y<2-z\land y+z\leq x\leq 2)\lor (y=2-z\land x=2))$$

I don't think that it's possible to solve for the domain in $(r,\xi,\eta)$ by $$x\to r \ \xi \ \sqrt{1-\eta^2}, y \to r \sqrt{1-\xi^2} \ \sqrt{1-\eta^2}, z \to r \ \eta $$ with $\xi, \eta$ representing the sines of the angles in spherical coordinates.

The cartesian integrals are trivial, eg the center of gravity is

$$\frac{\int_0^2 \left(\int_0^x \left(\int_0^{x-y} \{x,y,z\} \, dz\right) \, dy\right) \, dx}{\int_0^2 \left(\int_0^x \left(\int_0^{x-y} 1 \, dz\right) \, dy\right) \, dx} = \left\{\frac{3}{2},\frac{1}{2},\frac{1}{2}\right\}$$

coinciding with Mathematica

 Integrate[{x, y, z}, {x, y, z} \[Element] 
   Simplex[{{0, 0, 0}, {2, 0, 0}, {2, 2, 0}, {2, 0, 2}}]]/
 Integrate[  1, {x, y, z} \[Element] 
   Simplex[{{0, 0, 0}, {2, 0, 0}, {2, 2, 0}, {2, 0, 2}}]]

If you prefer spherical coordinates, choose $(2,2,0)$ as origin and the symmetry axis from $(2,2,0)$ to $(0,2,2)$ as the new z-polar axis with rotional symmetry by $\frac{2\pi}{3}$ for the former cartesian axes.