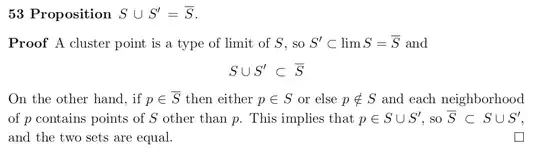5

In the following proof from Real Mathematical Analysis by Pugh, it is suggested that the open ball $M_{r/2}p$ is perfect. enter image description here

But if we consider a perfect set $S \subset M$, then $S = S'$ where $S'$ is the set of cluster points of $S$. Also based on the proposition below, $\overline S = S \cup S' = S' \cup S' = S' = S$, which means $S$ is closed in $M$. So how can $M_{r/2}p$ be perfect, while being an open set?

enter image description here

Also, A metric space $M$ is perfect if $M′=M$, i.e., each $p \in M$ is a cluster point of $M$.

MrAmbiguneDL
  • 305
  • The only way I can think of to construe this discussion as consistent is if one considers $M_{r/2}(p)$ and $\overline{M_{r/2}(p)}$ as subspaces (i.e., metric spaces in their own right) of the parent subspace. – triple_sec Dec 31 '24 at 06:02
  • 3
    You should add the definition of "perfect". It does not seem to be this : https://en.wikipedia.org/wiki/Perfect_set – Paul Frost Dec 31 '24 at 07:09
  • 2
    That's the point: in this book, "perfect" is not defined for subsets, but as a property of metric (or topological) spaces. – Ulli Dec 31 '24 at 08:52
  • 2
    Please edit your question to include this essential information. People do not want to read comments to get all relevant information. – Paul Frost Dec 31 '24 at 09:29
  • 1
    @MrAmbiguneDL I think you had full right to be confused by this, if I encountered such phrasing I'd be very confused myself. There is two notions of "perfect", a perfect subset of topological space, and a perfect topological space. And the author should, in my opinion, be aware of the difference, and distinguish the two. This is confusing for both people learning the topic, and people advanced into it. Instead I would call the set as in your book to be dense-in-itself – Jakobian Dec 31 '24 at 10:13
  • 1
    Please [edit] your question to include the definition of "perfect". This is important because, as others have noted, the word "perfect" is used in multiple different ways in mathematics (in topology, even). – Xander Henderson Dec 31 '24 at 20:58

1 Answers1

8

It seems that the phrase "perfect" is not standardized in the literature. Many authors (see e.g. Wikipedia) define a subset $S$ of a topological space $M$ to be perfect if $S$ is closed in $M$ and each $x \in S$ is a cluster point of $S$. This is a "relative concept" defined for subsets of an ambient space $M$.

Pugh introduces an "absolute concept" of a perfect space by requiring that all of its points are cluster points. No ambient space is involved here. For the sake of distinction let us use the phrase "a-perfect" in this case. This is just an ad hoc notation.

The relationship between the two concepts is simple:

  • A space $M$ is a-perfect if and only if $M$ is a perfect subset of itself.

  • Each perfect subset $S$ of a space $M$ is an a-perfect space when endowed with the subspace topology (for a metric space $M$, $S$ will be endowed with the metric inherited from $M$).

  • A subset $S \subset M$ which is an a-perfect space is not necessarily a perfect subset of $S$ because it may not be closed. As an example consider $S = (0,1) \subset M = \mathbb R$.

Here is your misunderstanding:

But if we consider a perfect set $S \subset M$, then $S = S'$ where $S'$ is the set of cluster points of $S$.

This is not true. The set $S'$ of cluster points of $S$ in $M$ is in general bigger than the set of cluster points of $S$ in itself - be aware of the conflict between the absolute and relative concepts of cluster points. Thus we have $S \subset S'$ for subsets which are a-perfect and $S = S'$ iff $S$ is closed and a-perfect.

psmears
  • 790
Paul Frost
  • 87,968
  • 2
    No need to introduce your own nomenclature, since the concept of dense-in-itself set exists – Jakobian Dec 31 '24 at 10:17
  • 1
    @Jakobian Correct, but I wanted to stay closely at Pugh's notation. Actually Pugh could have used "dense-in-itself" instead of "perfect". – Paul Frost Dec 31 '24 at 10:24
  • 1
    I think that's what he should have used, this type of confusion is possibly why the name "dense-in-itself" was invented. The way Pugh uses the word "perfect" is awful from educational perspective – Jakobian Dec 31 '24 at 10:27
  • 3
    @Jakobian: This is especially unfortunate in light of the fact that the standard notion of a perfect set is one that is both closed and dense-in-itself, where "closed" and "dense-in-itself" can be considered duel properties in a certain sense. The Cantor-Bendixson method (early 1880s), and the $1$-step condensation point method due to Lindelöf (1905), is a way of obtaining a perfect set "from above" (by removing points), while Hausdorff's dense-in-itself method (1914) is a way of obtaining a perfect set "from below" (by using the union of all dense-in-itself subsets). (continued) – Dave L. Renfro Dec 31 '24 at 11:43
  • 2
    These methods have been repeatedly and extensively generalized to provide a unified understanding of many other situations -- see this mathoverflow question/answers and this MSE answer. – Dave L. Renfro Dec 31 '24 at 11:43
  • @Jakobian Usually one finds the definition of a dense-in-itself subset of a space $X$. This is again a "relative" definition, although the property of being dense-in-itself is an "absolute " property of a space. Perhaps this is why Pugh chose his notation? – Kritiker der Elche Jan 01 '25 at 10:07
  • @KritikerderElche It's not notation but nomenclature. And I don't see how what you said justifies the choices made by Pugh here. Nothing that you said gives a reason for why one would choose this nomenclature. – Jakobian Jan 01 '25 at 10:16
  • 1
    A Google search shows that Pugh's use of "perfect" is not an isolated case (which does not mean it is a good choice). See e.g. nLab. Even more confusing, some authors define a perfect space to be a $G_\delta$-space. See https://en.wikipedia.org/wiki/Perfect_set for a discussion. – Paul Frost Jan 01 '25 at 23:50