7

Background: this came from a casual discussion about the compound interest problem.

Consider the function $f(a,b),a\in\Bbb N, b\in\Bbb R\setminus\{0\}$ where

$f(0,b)=1+\frac{1}{b}$,

for $a\neq 0$, $f(a,b)=f(a-1,b)^{f(a-1,b)}$

Question: What is $\lim_{n\to \infty}f(n,n)$? What is the speed of convergence w.r.t. $n$, i.e. $O(|f(n,n)-\lim_{m\to \infty}f(m,m)|)$?

My attempt:

The Mathematica code below should calculate the desired function correctly:

Seq = {};
For[n = 10, n <= 10000, n = n + 50,
  temp = 1 + 1/n;

For[i = 1, i <= n, i++,
   temp = Power[N[temp, 20], N[temp, 20]];
   ];


AppendTo[Seq, {n, temp}];
  ];
ListPlot[Seq]

which gives $f(n,n)$ w.r.t. $n$: 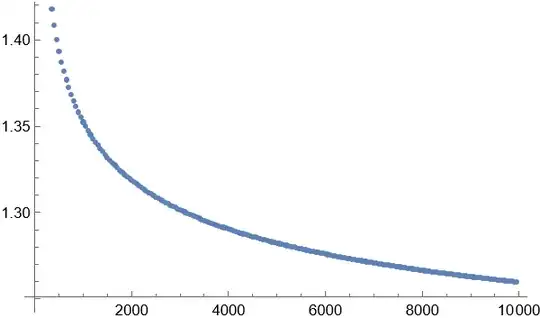f(n,n) w.r.t. n

And hence I highly suspect that it converges. Taking $g(a,b)=\ln f(a,b)$ just gives $g(a,b)=g(a-1,b)\exp g(a-1,b)$ which does not quite simplify the structure.

José Carlos Santos
  • 440,053
Ma Ye
  • 577
  • 1
    by trial an error I tried $f(x)=10.4/\ln(x)$ and kind a suits (I look for $a/\ln(3000) = 1.3\Rightarrow a\approx 10.4$ from the points in the graph)... Did you tried it? – Joako Dec 28 '24 at 19:30
  • 2
    My computer calculations suggest that $\lim_{n\to\infty} f(n,n)=1$. – Alex Ravsky Dec 28 '24 at 19:39
  • This is quite an interesting function. When you take it's natural logarithm, you get a tower of fractals. –  Dec 29 '24 at 10:33
  • I suspect it goes to 1 –  Dec 29 '24 at 11:15
  • 1
    Quite surprizing $f(x) \sim 1+\frac{1+\sqrt{2}}{\log (x)}$ – Claude Leibovici Jan 01 '25 at 08:00
  • $f(n,n)$ is decreasing since $1+\frac{1}{n}<\left(1+\frac{1}{n}\right)^{1+\frac{1}{n}}<1+\frac{1}{n-1}$. If you can find a sufficiently sharp upper bound (this bound is too loose) on $x^x$ that's easier to work with, you might be able to show that $f(n,n)$ is upper-bounded by a function going to $1$. – Varun Vejalla Jan 02 '25 at 02:11
  • @ClaudeLeibovici How did you get that asymptotic? –  Jan 02 '25 at 12:58
  • @AkshajMishra. It is not an asymptotic but just a guess after a quick and dirty linear regression. Happy New Year ! – Claude Leibovici Jan 02 '25 at 13:02

1 Answers1

1

I do not have the strength to write what would be needed, but I got $$\ln f(3,b) = (e^k)^{e^k} * e^k * k$$ and $$\ln f(4,b) = (e^k)^{{(e^k)}^{{(e^k)}^{e^k}}} * (e^k)^{e^k} * e^k * k$$ where $$k=(1+\frac{1}{b})\ln(1+\frac{1}{b})$$ I doubt this pattern is very hard to prove using induction, and once that is done, if $b\to\infty$ then $k\to0$ and hence $\ln f(n,n) \to 0$ from which we get $$\lim_{n\to\infty}f(n,n) = 1$$

Edit: I realized the pattern might be hard to see from just two examples, so the pattern is that the highest tower has $2^{n-2}$ terms for $f(n,b)$, and the towers after that have $2^{n-3}, 2^{n-4}, \dots$ terms.

  • It somehow makes sense, but I think you need to formally prove that taking the limit of k before the tower indeed works correctly. – Ma Ye Dec 29 '24 at 13:47
  • Why can't we just assume that they are just large values of $b$ then BAM! You reveal to the math gods that this was a buildup to the limit. –  Dec 29 '24 at 13:53
  • I'd like to see a proof. The problem is that $k$ is close to $0$, but the exponential tower is super high which moves it away from $1$. As an example, $(1+\frac{1}{n})^{(1+\frac{1}{n})} \approx (1+\frac{1}{n}) + e^{\frac{1}{n}} (e^{\frac{1}{n^2}}-1)$. This process is carried out $n-1$ more times, getting larger each time. – The Other Terry Dec 29 '24 at 23:00
  • If you use $(a^b)^c = a^{bc}$ then if $k$ goes to $0$ then the tower virtually disappears. To add to that, you have the $k$ multiplied by everything at the end, so that helps to make everything go to $0$. Apart from that, I have no idea how a formal proof can be constructed –  Dec 30 '24 at 04:16