0

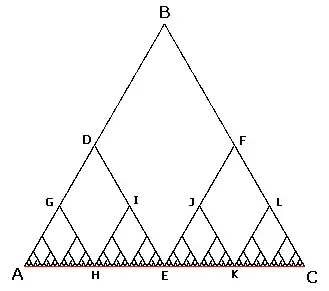
$ABC$ is an equilateral triangle.

enter image description here

The path $ABC$ is twice as long as $AC$. Similarly the path $ADEFC$ is also twice as long as $AC$, as is the path $AGHIEJKLC$, and so on. Breaking down the jagged path into smaller and smaller jags, the deviation of the jaged path from the straight line $AC$ goes to zero, so, in a sense, the line $AC$ is the "limit" of the sequence of jagged paths. This seems to suggest that the length of $AC$ is twice the length of itself!

This is obviously wrong, but why$?$

Blue Cat Blues
  • 10,058
  • 2
    Related: https://www.reddit.com/r/learnmath/comments/188d12g/so_whats_the_actual_explanation_of_why_proof_that/?rdt=46200 – Davide Masi Dec 23 '24 at 19:55
  • 1
    "In a sense" it's the limit. But it's not the right sense. – Robert Israel Dec 23 '24 at 20:07
  • The answer is simply that this notion of length is not preserved under this notion of limit. There is no reason to expect this to be true. – Smiley1000 Dec 23 '24 at 20:37
  • The curve approximating the line is not differential/smooth. This leads to some fractal effects that can cause things like this to happen. It's like the proof that $pi$ is 4: https://math.stackexchange.com/questions/12906/the-staircase-paradox-or-why-pi-ne4 – TurlocTheRed Dec 23 '24 at 22:03

2 Answers2

5

Let us add Cartesian coordinates so that $A=(0,0),$ $B=(\frac12, \frac12\sqrt{3}),$ and $C=(1,0).$

The length of the graph of a smooth function $f:[0,1]\to\mathbb R$ is given by $$ L[f] = \int_0^1 \sqrt{1+f'(x)^2}\,dx. $$

We have a sequence of functions $f_n:[0,1]\to\mathbb R$ with $f_1$ having $ABC$ as graph, $f_2$ having $ADEFC$ as graph, and so on. We notice that for all $n$ we have $$ L[f_n] = \int_0^1 \sqrt{1+f_n'(x)^2}\,dx = 2. $$

But we also have pointwise convergence $f_n(x)\to z(x) := 0$ for all $x\in[0,1]$ as $n\to\infty$ and $$ L[z] = \int_0^1 \sqrt{1+z'(x)^2}\,dx = 1. $$

The paradox then is that $L[f_n] \not\to L[z]$ although $f_n \to z.$

The solution to the paradox is that although $f_n\to z$ we do not have $f_n' \to z'.$ Therefore the integral for $L[f_n]$ does not converge to the integral for $L[z].$

md2perpe
  • 30,042
  • 1
    This is the sort of the answer I was thinking of writing, but I don't quite agree with your logic. What you write is about the failure of a sufficient condition for convergence of length: that theorem (convergence of derivatives implies convergence of length) doesn't apply, and so one would not expect convergence. But it does not imply failure of convergence. – Lee Mosher Dec 23 '24 at 21:08
  • Are the vertices not a problem for the differentiability of $f_n$? – Davide Masi Dec 23 '24 at 21:28
  • 1
    @LeeMosher. We have $|f_n'|=\sqrt3$ so $L[f_n] = \int_0^1 \sqrt{1+(\sqrt 3)^2},dx.$ How could this possibly converge to $L[z] = \int_0^1 \sqrt{1+0^2},dx$? – md2perpe Dec 23 '24 at 21:30
  • 1
    @DavideMasi. Yes, the vertices are a problem. The correct statement should be that if $f$ is piecewise smooth, say on the intervals $[a_0:=0,a_1), (a_1, a_2), \ldots, (a_{n-1}, a_n:=1],$ then the length of the graph is given by $$\sum_{k=0}^{n-1} \int_{a_k}^{a_{k+1}} \sqrt{1+f'(x)},dx.$$ This can be written as $\int_0^1 \sqrt{1+f'(x)^2},dx$ where we just exclude the problematic points. – md2perpe Dec 23 '24 at 21:40
  • @mt2perpe: To clarify, my remarks were about your final paragraph. Namely, the convergence property $f'_n \to z'$ mentioned in that paragraph is a sufficient condition in general for the convergence property $L[f_n] \to L[z]$, but it is not a necessary condition. – Lee Mosher Dec 24 '24 at 22:30
  • @LeeMosher. I get it. In general it is not even the case that $f_n\to z$ implies $\int F(f_n(x)), dx\to \int F(z(x)), dx,$ less so that $\int F(f_n'(x)),dx\to \int F(z'(x)),dx.$ – md2perpe Dec 25 '24 at 09:33
0

This is very similar to an argument where $\pi = 4$, where you take a circle of radius $1$ inscribed in a square with side lengths of $2$ and flip inside each of the corners repeatedly until the square approaches the shape of the circle. Of course, $\pi$ isn't $4$. The flaw in this reasoning is that, in terms of length, increasingly small jagged edges under a limit are fundamentally distinct from smooth curves and lines.

The point of a limit is that it should approach the target value over time. However, in this process, the length of the jagged line does not get any closer to $AC$ under any number of iterations since it is constant. Therefore, interpreting the limit as equal to $AC$ is incorrect.

Hayden Taylor
  • 11