Consistent and inconsistent systems of linear equations over $\mathbb{Z}_2$

Question

I was wondering about the following question: Let's consider all possible systems of linear equations over $\mathbb{Z}_2$ which have size $n \times n$. By that, I mean such systems: $$Ax=b, \quad A \text{ is an $n \times n$ matrix with elements $a_{ij} \in \mathbb{Z}_2$, b is also a column of $b_i \in \mathbb{Z}_2$} $$

So, I wonder which systems are more: consistent or inconsistent?

The only thing I've been able to come up with is that it's almost obvious that matrices with non-zero determinant are less than matrices with zero determinant. But that gives me nothing considering my initial question because matrices with non-zero determinant always give a consistent system, but matrices with zero determinant may give both a consistent or an inconsistent one.

Answer 1

Here's a discussion for $n > 10$ (informally, "large $n$"). Sadly, it stalls out short of a conclusion, but it makes at least some progress.

Consider a rank-$p$ matrix $A$ with $0 \le p < n$.

The column-space is $p$ dimensional, so has $2^p$ elements (pick a basis of $k$ columns, assign a 1 or 0 as coefficient to each).

Now let's look at some values of $b$ that make this consistent. Because the first $p$ vectors form a basis, they span a subspace of $2^p$ points of $F^n$, so there are $2^p$ 'good' target vectors. For each of these, there may be a great many solutions (i.e., $x$-vectors), but we don't care about that. What this means is that there are $2^n - 2^p \ge 2^{n-1}$ values of $b$ for which the system is inconsistent. (or, on the positive side, $2^p$ for which it's consistent). Put differently, the majority of such systems are inconsistent, with the probability of inconsistency rising rapidly as the rank decreases.

But... for $p = n$ ... well, for those, all values of $b$ are consistent. And there are a lot of them.

Letting $N(p)$ denote the number of matrices of rank $p$, we get that the number of consistent systems is $$ N(0)2^0 + N(1) 2^1 + N(2) 2^2 + \ldots N(n-1) 2^{n-1} + N(n)2^n $$ and the question is "is this more or than half of $2^{n^2 + n}$ (the total number of size-$n$ systems), i.e., is it more than $2^{n^2 + n - 1}$?

It turns out that $N(n)$ (for large $n$) is about $0.28 \cdot 2^{n^2}$ (see this answer).

If I've done my algebra right, then if the fraction of rank=$n-1$ matrices is less than 16%, then in fact there are more "inconsistent" than consistent systems.

The opposite conclusion is not valid -- the 16% number is based on a very crude estimate, i.e., that for all matrices with rank less than $n-1$, at least $3/4$ of systems are inconsistent (but for most ranks, it's a much larger fraction!), while for those with rank = $n-1$, half are.

One could also look at those with rank less than $n-2$, for which at least $7/8$ are inconsistent. But then you'd need to estimate both $N(n-1)$ and $N(n-2)$.

Sadly, I don't see an easy way to imitate Joriki's method for those cases. There are just too many ways for a matrix to have rank $n-1$ or $n-2$ to allow for easy counting.

Answer 2

I thought about this one before bed last night, and realized there was a nice recurrence (albeit one I cannot solve...but I can write a program!).

Consider $$ Ax = b $$ for some particular $A$ and $b$. This is consistent exactly when $b$ lies in the span of the columns of $A$.

If $A$ has rank $r$, this span has exactly $2^r$ vectors in it.

So if we can compute, for each rank $r$ from $0$ to $n$, how many matrices have rank $r$, and for each of these how many $b$-values work, we'll know the count $C$ of how many consistent systems there are. We'll do that presently.

The total number of such systems is $2$ to the number of variables...and there are $n^2$ of these in $A$, and $n$ more in $b$. So the fraction of systems that are consistent is exactly $$ \frac{C}{2^{n^2 + n}}. $$

How can we compute $C$? Let's first compute, for each rank $r$, how many matrices $A$ have rank exactly $r$. To do that, I'm going to look first at $n \times k$ matrices, and ask "how many of these have rank $r$?" The simple answers are

1. If $k = r = 0$, then it's 1: the empty matrix has rank 0.

2. if $k = 0$ and $r > 0$, it's zero. A no-column matrix can't have positive rank. This is a special case of...

3. If $r > k$, then it's 0: a 3-column matrix can't have rank 4.

4. if $r = 0$ and $k > 0$, then it's 1: an all-zero matrix has rank 0, and there's only one of these.

Now let's ask about the nontrivial case, where $k$ and $r$ are both nonzero, and $r \le k$. So we have an $n \times k$ matrix we're looking at. Let's regard it as having been created from an $n \times (k-1)$ matrix $M$ by adding in a last column, $v$. We divide into two cases:

1. $M$ has rank $r$ already. In this case, $v$ must be in the span of the columns of $M$, or it would increase the rank. That span has $2^r$ vectors in it.

2. $M$ has rank $r-1$. In this case, $v$ must be in the complement of the span of $M$'s columns. There are $2^n - 2^(r-1)$ such vectors.

Let's let $U(n, r, k)$ denote the number of $n \times k$ matrices of rank exactly $r$. The preceding tells us that

1. $U(n,0, 0) = 1$, (the empty matrix)

2. $U(n, 0, k) = 1$ (the all-zero matrix)

3. $U(n, r, k) = 0$ if $r > k$.

4. $U(n, r, 0) = 0$ for $r > 0$ because an empty matrix can't have positive rank,

5. in the remaining cases, $U(n, r, k) = (2^n - 2^{r-1}) U(n, r-1, k-1) + 2^r U(n, r, k-1)$.

It's easy to write a recursive program to evaluate these numbers, and in DrRacket, which happily performs arithmetic on integers with hundreds or thousands of digits, I didn't have to do anything clever to do so.

For a given $n$, looking at $U(n, r, n)$ for $r = 0, \ldots, n$, divided by $2^{n^2 + n}$, shows the probability of an $n \times n$ matrix in $F_2$ having each possible rank. Here are some results, truncated to 3 decimal digits for easy viewing:

n = 2:
(.062 .562 .375)
n = 3
(.002 .096 .574 .328)
n = 4
(0.0 0.003 0.112 0.577 0.308)
n = 10
(0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.005 0.128 0.578 0.289)
n = 20
(0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
 0.0 0.0 0.0 0.0 0.0 0.0 0.005 0.128 0.578 0.289)

As you can see, there's a huge concentration at rank $n$ and $n-1$, growing tighter as $n$ grows.

To determine the count of "consistent" systems, we can multiply the count of rank $r$ matrices by the number, $2^r$ of target vectors ($b$) in the span of any such matrix, and sum up. If we then divide by $2^{n^2 + n}$, we'll get the fraction of systems that are consistent.

Here are the results for $n = 2$ through $20$:

 #i0.75
 #i0.671875
 #i0.639404296875
 #i0.624476432800293
 #i0.6173064960166812
 #i0.613791377609914
 #i0.6120508501873964
 #i0.6111847920751259
 #i0.6107528079660376
 #i0.6105370763472455
 #i0.6104292755470074
 #i0.6103753913867268
 #i0.6103484533649911
 #i0.6103349853685301
 #i0.6103282516238772
 #i0.610324884814942
 #i0.6103232014263218
 #i0.6103223597359735
 #i0.6103219388917898
 #i0.6103217284699456)

(The #i means "this is an inexact number," i.e., a numerical approximation of the value.)

As you can see, it sure looks as of about 61% of all size-$n$ linear systems over $F_2$ are consistent for $n > 5$. I'm pretty sure that with the recurrence I've got, I could make an actual proof of this, but I'm out of energy for this problem.

I confess I was surprised. In my earlier answer, I showed that if not too many matrices had rank $n-1$, the "inconsistent" systems would win. What happened instead is that the concentration of matrices in the rank-$n$ and rank-(n-1) bins got greater and greater, while I had expected some spreading-out of the probabilities.

Live and learn, I guess!

Answer 3

A final answer, which shows that in fact the majority of linear systems are consistent.

In everything that follows, we're working over $\mathbb F_2$, the field with 2 elements.

Following Joriki, we define $j(n)$ to the be probability that an $n \times n$ random matrix over $F_2$ has full rank, i.e., rank $n$, i.e., $n$ independent columns. Let's look at $n = 4$, i.e., a $ 4 \times 4$ matrix of zero 0s and 1s. The first column will be dependent $1$ times (when it's all zeros), hence independent $2^4 - 1 = 15$ times, so the probability that it's independent is $$ \frac{15}{16}.$$ The second vector will be independent of the first if it's not in the span of the first, which has 2 items, i.e., $\frac{14}{16} = \frac{7}{8}$ of the time, so the probability that the first two are independent is $$ \frac{15}{16}\cdot\frac{7}{8}. $$ The third will be independent of the first two if it's not in their span, which has four elements, i.e., $\frac{12}{16} = \frac{3}{4}$ of the time, and the fourth will be independent of the first three $\frac{1}{2}$ of the time. So $$ j(4) = 1 \cdot \frac{15}{16}\cdot\frac{7}{8}\cdot\frac{3}{4}\cdot\frac{1}{2} $$ where I've thrown in a factor of $1$ at the front, and I'll call that $j(0)$. You can easily see that in general $$ j(n) = \frac{2^n - 1}{2^n} j(n-1) \tag{1}. $$ We can generalize to give our partial computations names. We'll define $J(n, k)$ (for $n \le k)$ to be the probability that an $n \times k$ matrix has rank $k$, and from the pattern above, infer that $$ J(n, k) = \frac{2^{n+1-k} - 1}{2^{n+1-k}} \cdot J(n, k-1). $$ In particular, note that $$ J(n, n) = \frac{1}{2} J(n,n-1) $$ and $$ J(n, n) = \frac{3}{4}\cdot \frac{1}{2} J(n, n-2) $$ or, inverting things, $$ J(n, n-1) = 2 J(n,n) \\ \tag{j1} $$ and that $$J(n, n-2) = \frac{8}{3} J(n, n) \tag{j2} $$

Now (for $r \le k$) define $F(n, k, r)$ to be the fraction of all $n \times k$ matrices that have rank $r$ (and define it to be zero for $r > k$). As in the previous answer discussing the number of such matrices, there's a recurrence for $F$ namely $$ F(n, k, r) = \begin{cases} 2^{-nk} & r = 0 \\ 0& k = 0, r > 0 \\ 0 & r > k \\ (1 - 2^{-(n-r+1)}) F(n, k-1, r-1) + 2^{-(n-r)} F(n, k-1, r) & \text{otherwise} \end{cases} \tag{f1} $$ We can compute an explicit table of $F(n, k, r)$-values for $n = 5$, for example:

1.0000         0         0         0         0         0
0.0312    0.9688         0         0         0         0
0.0010    0.0908    0.9082         0         0         0
0.0000    0.0066    0.1987    0.7947         0         0
0.0000    0.0004    0.0310    0.3725    0.5960         0
0.0000    0.0000    0.0043    0.1203    0.5774    0.2980

where the row index is the number $k$ of columns, and the column index is the rank $r$, and both run from $0$ to $5$. We see that a $5 \times 5$ matrix has about a 30% change of being invertible.

The entries along the diagonal are just $j(0), j(1), \ldots, j(5)$, as you can see by comparing the definitions of $j$ and $F$.

You can see that the next-to-last diagonal entry, 0.5960 is about twice the last one, 0.2960, and that's no coincidence: it follows from equation j1; similarly, the $0.7947$ is $\frac{8}{3}$ of 0.2960, which follows from equation j2. If we replace that bottom-right entry with "c", we now have

(8/3)c         0         0
0.3725        2c         0
0.1203    0.5774         c

Note to the reader: I focused on this 3 by 3 block of the table after lots of simulations and experiments on the computer showed me that most of the consistent systems, for any $n > 3$ were represented by data in this block. For those with $n \le 3$, we can check the claim by hand. Now, back to the exposition.

The recurrence for $F$, in Equation f1, show that each value in this table can be computed as a linear combination of the one above, and the one above-and-to-the-left. Here's that same statement, with the coefficients filled in from Equation f1, but with the numerical values replaced by symbols so that we're not stuck on the $n = 5$ case:

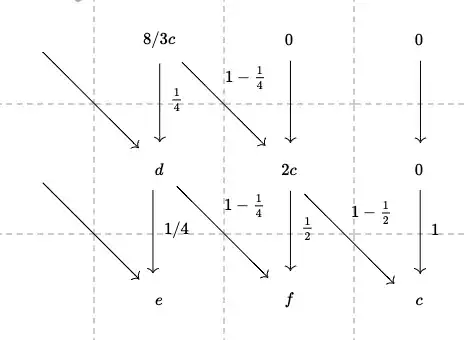
(Diagram source here.)

Now we can estimate $d, e,$ and $f$ as follows. First, $d$ is a sum of $2c/3$ and something else, so we have $d > \dfrac{2c}{3}$. Similarly, $e$ is at least $\dfrac{1}{4}$ of $d$, so $e > \dfrac{c}{6}$. And finally, \begin{align} f &= \frac{1}{2} 2c + (1 - \frac{1}{4}) d \\ &> c + \frac{3}{4} \frac{2c}{3} \\ &> c + \frac{c}{2} = \frac{3}{2}c \end{align} So the last three entries in the last line of that table are at least $$ \pmatrix{\frac{c}{6} & \frac{3}{2}c & c }. $$

In other words, $c$ of the matrices have full rank, at least $3c/2$ have rank $n-1$ and at least $\dfrac{c}{6}$ have rank $n-2$.

Now let's look not just at matrices, but at systems of equations, i.e., pairs $(A, b)$ where $A$ is an $n \times n$ matrix and $b$ is an $n$-vector, and the system they represent is $$ Ax = b. $$ This system is consistent (i.e., has a solution) exactly if $b$ is in the column space of $A$, so if $A$ is full-rank, then any system $(A, b)$ is consistent. If $A$ has rank $n-1$, then the column space of $A$ is exactly half of the $2^n$ items in $\mathbb F^n$, so there are $2^{n-1}$ vectors $b$ with $(A, b)$ being consistent. And if $A$ has rank $n-2$, then only a quarter of all target vectors lie in its column spaces, so there are $2^{n-2}$ systems $(A, b)$ that are consistent.

Summing these facts up, the last three entries in our table correspond to a total of $$ 2^{n-2} 2^{n^2}e + 2^{n-1} 2^{n^2} f + 2^n 2^{n^2}c $$ consistent systems. As a fraction of the $2^n \cdot 2^{n^2}$ systems overall, we find that the consistent systems constitute at least a fraction $$ \begin{align} K &= \frac{2^{n-2} e + 2^{n-1} f + 2^n c}{2^n} \\ &= e/4 + f/2 + c \\ &> \frac{c}{24} + \frac{3c}{4} + c \\ &= \frac{43c}{24} \\ \end{align} $$

Fortunately, it's easy to see that $j$ is a decreasing function of $n$, and given that its limit as $n \to \infty$ is slightly more than $28.8$, we can estimate to see that $$ K = \frac{43}{24} c > \frac{43}{24} \cdot 28 = 50 ~ \frac{1}{6}, $$ so in fact more than half of all linear systems over $\mathbb F_2$ are in fact consistent!