Prove a quartic curve intersect a circle at four points and orthogonally

Question

This page mentioned that

Distance between the Feuerbach point $F$ and the midpoints $M, E,$ and $D$ of the sides satisfy $FM=FD+FE$.

It is also mentioned in MathWorld entry Feuerbach Point

If $F$ is the Feuerbach point a triangle $\triangle A B C$ and $X, Y$, and $Z$ are the midpoints of the sides $B C, C A$, and $A B$, respectively, then one of the distances $|F X|,|F Y|$, and $|F Z|$ is equal to the sum of the two others.

It is also used in 5# of this thread

by the property of Feuerbach point $FeM + FeN =FeL$...(2)(letting $FeL$ the maximum of three lines that feuerbach point is connected to points of medial triangle)

I didn't find proofs of this fact in the above three sources.

I found online a proof in the PDF "Casey’s Theorem and its Applications" (Link 1 or Link 2)

VI) △ABC is scalene and D, E, F are the midpoints of BC, CA, AB. The incircle (I) and 9 point circle ⊙(DEF) of △ABC are internally tangent through the Feuerbach point Fe. Show that one of the segments FeD, FeE, FeF equals the sum of the other two.

I rephrased the proof below:

Lemma. The two circles are tangent at $T$.
Draw a tangent line $AB$ from the moving point $A$ on the larger circle to the smaller circle.
Then $AT/AB=\sqrt{R/(R-r)}$ is constant (independent of $A$).

In the figure below, let $Fe$ be the Feuerbach Point of a triangle $ABC$, the incircle touches the sides at $D,E,F$, the midpoint of the sides are $L,M,N$.

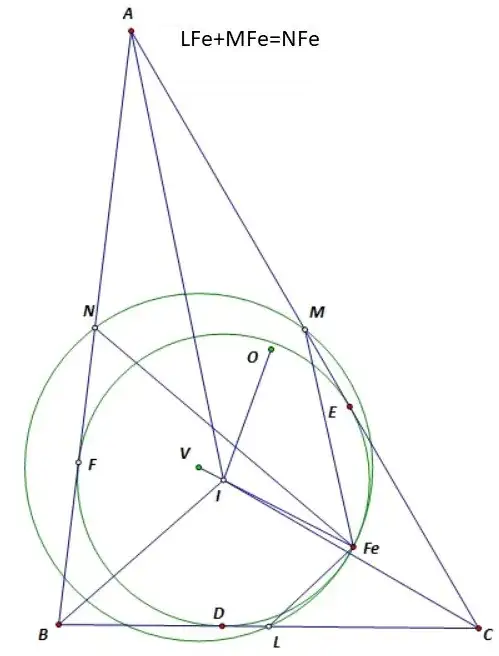
By the lemma, $LFe/LD=MFe/ME=NFe/NF$. So it suffices to prove $LD+ME=NF$.

But $DL=\frac{A C-A B}{2}$, $EM=\frac{B C-A C}{2}$, $NF=\frac{A B-B C}{2}$, so we proved $LD+ME=NF$, hence $LFe+MFe=NFe$.

---

My question: Is the converse true? That is, $P$ is a point on the nine-point circle such that one of $PD, PE, PF$ equals the sum of the other two, where $D,E,F$ are midpoints of the sides, then $P\in\{Fe,Fe_a,Fe_b,Fe_c\}$? where $Fe$ is the Feuerbach point, $Fe_a,Fe_b,Fe_c$ are the ex-Feuerbach points.

The locus of $P$ such that $PD±PE±PF=0$ is a quartic curve $\cal C$. Need to prove the intersection of it and the circumcircle of $DEF$ is $\{Fe,Fe_a,Fe_b,Fe_c\}$. Also, they seem to intersect orthogonally. So my question is,

Let $D,E,F$ be three points on a circle $\cal C$. The locus of $P$ such that $PD\pm PE\pm PF=0$ is a quartic curve $\cal Q$. How do you prove $\mathcal C\cap\mathcal Q$ is four points? Also, do they intersect orthogonally at each of these points?

In general, do a bicircular quartic and a circle intersect in 4 points, counted with multiplicity and with the circular points deducted?

By Ptolemy's Theorem $P\in\cal C$ is equivalent to $PD\cdot EF\pm PE\cdot DF\pm PF\cdot DE=0$.

Eliminating $PF$ from $PD\pm PE\pm PF=PD\cdot EF\pm PE\cdot DF\pm PF\cdot DE=0$ we get the value of $PD/PE$, so an Apollonian circle wrt $D,E$ intersects $\cal C$ orthogonally at $P$.

Answer 1

The problem can be rewritten as follows:

Given an inequilateral triangle $ABC$

(i) The locus of points $P$ such that one distance in $\left\vert{PA}\right\vert, \left\vert{PB}\right\vert, \left\vert{PC}\right\vert$ is equal to the sum of the others is a bicircular quartic $\mathcal{Q}$.

(ii) $\mathcal{Q}$ intersects the circumcircle of triangle $ABC$ at 4 real points.

(iii) (conjecture) $\mathcal{Q}$ is orthogonal to the circumcircle of triangle $ABC$ at those 4 real points.

So far, I can only prove (i) and (ii).

Let's use the barycentric coordinate system where $ABC$ is the reference triangle. Denote by $a, b, c$ the lengths of $BC, CA, AB$. one distance in $\left\vert{PA}\right\vert, \left\vert{PB}\right\vert, \left\vert{PC}\right\vert$ is equal to the sum of the others if and only if

$$ (\left\vert{PA}\right\vert + \left\vert{PB}\right\vert + \left\vert{PC}\right\vert)(-\left\vert{PA}\right\vert + \left\vert{PB}\right\vert + \left\vert{PC}\right\vert)(\left\vert{PA}\right\vert - \left\vert{PB}\right\vert + \left\vert{PC}\right\vert)(\left\vert{PA}\right\vert + \left\vert{PB}\right\vert - \left\vert{PC}\right\vert) = 0 $$

which is equivalent to

$$ 2({\left\vert{PA}\right\vert}^{4} + {\left\vert{PB}\right\vert}^{4} + {\left\vert{PC}\right\vert}^{4}) = {({\left\vert{PA}\right\vert}^{2} + {\left\vert{PB}\right\vert}^{2} + {\left\vert{PC}\right\vert}^{2})}^{2} $$

Let $P = (x : y : z)$ then

$$ {\left\vert{PA}\right\vert}^{2} = \frac{c^{2}y^{2} + b^{2}z^{2} + (b^{2} + c^{2} - a^{2})yz}{{(x + y + z)}^{2}}, \quad {\left\vert{PB}\right\vert}^{2} = \frac{a^{2}z^{2} + c^{2}x^{2} + (c^{2} + a^{2} - b^{2})zx}{{(x + y + z)}^{2}}, \quad {\left\vert{PC}\right\vert}^{2} = \frac{b^{2}x^{2} + a^{2}y^{2} + (a^{2} + b^{2} - c^{2})xy}{{(x + y + z)}^{2}}. $$

By substitution, we obtain a homogeneous quartic equation of $x, y, z$. Here I make use of SymPy to simplify the equation

from sympy import *
a, b, c, x, y, z = symbols("a b c x y z", real=True)
a is BC^2
b is CA^2
c is AB^2
P = 2 * ((c * y ** 2 + b * z ** 2 + (b + c - a) * y * z) ** 2 + (a * z ** 2 + c * x ** 2 + (a - b + c) * z * x) ** 2 + (b * x ** 2 + a * y ** 2 + (a + b - c) * x * y) ** 2) - (c * y ** 2 + b * z ** 2 + (b + c - a) * y * z + a * z ** 2 + c * x ** 2 + (a - b + c) * z * x + b * x ** 2 + a * y ** 2 + (a + b - c) * x * y) ** 2
factor((P + 3 * (a * y * z + b * z * x + c * x * y) ** 2))

The quartic equation is quite long. However, I managed to rewrite it into the form

$$ f(x, y, z) \times (x + y + z) - 3{(a^{2}yz + b^{2}zx + c^{2}xy)}^{2} = 0 $$

where $f$ is a cubic homogeneous polynomial of $x, y, z$ (uncomment the last line of the above snippet and run to see its full form)

In this barycentric coordinate system, the coordinates of circular points satisfy $a^{2}yz + b^{2}zx + c^{2}xy = x + y + z = 0$ as they are the intersection of the line at infinity and any circle. Together with the above equation, we can deduce that the quartic is bicircular (if we substitute $z = -x - y$ then the newly obtained equation has two solutions of multiplicity two, which correspond to the two circular points).

The circumcircle of triangle $ABC$ (a plane algebraic curve of degree 2) and the above quartic (a plane algebraic curve of degree 4) have 8 intersections (counted with multiplicity and including complex points) according to Bezout's theorem. On the other hand, two circular points are their intersections (each has multiplicity two) so the circumcircle of triangle $ABC$ and $\mathcal{Q}$ have at most 4 real intersection points. In the question, @hbghlyl proved geometrically (in the question) that there are 4 points on the circumcircle that satisfy the equation, hence $\mathcal{Q}$ and the circumcircle of triangle $ABC$ have 4 real intersection points.

Comment: The above proof works for scalene triangles only, as 4 Feuerbach points are distinct if and only if the triangle is scalene.

Answer 2

@DuongNgo's answer proved (i) and (ii).

Here is a proof of (iii):

(iii) Q is orthogonal to the circumcircle of triangle ABC at those 4 real points.

Take the component $PA-PB-PC=0$ as an example

As shown in the figure above, let $P$ be a moving point on the locus of $PA-PB-PC=0$, and its velocity is $\mathbf v$, then the magnitude of its velocity component on $AP$ is $v\cos\bigl\langle\mathbf v,\vec{AP}\bigr\rangle$, and the same is true for the other two. Since the locus makes $PA-PB-PC$ a constant, the three velocity components must satisfy $$v\cos\bigl\langle\mathbf v,\vec{AP}\bigr\rangle-v\cos\bigl\langle\mathbf v,\vec{BP}\bigr\rangle-v\cos\bigl\langle\mathbf v,\vec{CP}\bigr\rangle=0$$ Therefore, to prove that the locus is orthogonal to the circle, we need to prove the following geometry problem:

As shown in the figure below, there are four points $A$, $B$, $C$, $P$ on the circle $O$ that satisfy $PA-PB-PC=0$. Then $\cos\angle APO-\cos\angle BPO-\cos\angle CPO=0$. Proof: Let the radius of the circle be $R$, then obviously $PA=2R\cos\angle APO$, etc. Substituting in the equation, we get the result.