1

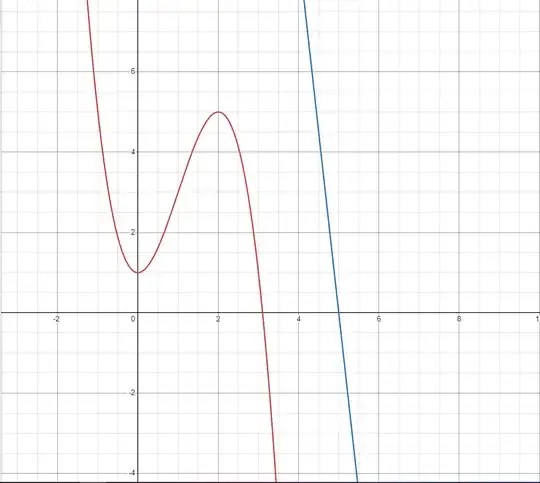
So I got this problem: What is the shortest distance between $f(x)=-x^3+3x^2+1$ and $g(x)=-9x+45$ on the interval $(0,+\infty)$. Two graphs

Obviously I can use the distance formula here, but the point on $f(x)$ that satisfy the shortest distance ($x=3$) is also where the tangent line of $f(x)$ is parallel to $g(x)$ and the distance is their common normal. I want to prove this generally for all cases, but what happens if the two graphs don't intersect on the interval $(a,b)$, but intersect right outside the interval? Is this still true? Example

Is there any condition for this to be true?

Andrei
  • 39,869
Phạm Minh Hoàng
  • 11
  • 3
  • Please clarify your specific problem or provide additional details to highlight exactly what you need. As it's currently written, it's hard to tell exactly what you're asking. – Community Dec 19 '24 at 13:29
  • I want to find a general solution for the problem: find the shortest distance between a curve and a line on an interval that they don't intersect. Is "the shortest distance is their common normal" true for all cases? – Phạm Minh Hoàng Dec 19 '24 at 13:52

1 Answers1

1

You need to check the ends of the intervals as well. Use a simple example something like two straight lines. If I use the same interval, $[0\infty)$, then a simple example is $y=0$ and $y=x+1$. They don't have a common normal, so the shortest distance happens at the end of the interval.

Even better, let the interval be $[-1.1,1.2]$ and the functions $y=x^2$ and $y=x^4+1$. The graph of these looks like

enter image description here

The common normal is at $x0$, where the distance is $1$, but you need to check the ends $x=-1.1$ and $x=1.2$. I've specifically used different distances from $0$ for the end of the intervals, just to show that you need to check both. See what would happen if the lower end is $-1.25$, $-1$, or $-0.5$.

Andrei
  • 39,869