How to set the limits of a definite integral by substitution?

Question

A worked example in my calculus textbook is to evaluate $$\int_0^\pi\sqrt{1-\sin2x}\text dx.$$ The book's approach is to use trig identities, but my idea is to use a substitution by letting $$t=1-\sin2x,$$ but I don't know how to set the limits. I calculated the indefinite integral as follows: $$x=\frac12\arcsin(1-t),\qquad\frac{\text dx}{\text dt}=-\frac1{2\sqrt{1-(1-t)^2}}.$$ $$\begin{align*} \int\sqrt{1-\sin2x}\text dx&=\int-\frac{\sqrt t}{2\sqrt{1-(1-t)^2}}\text dt\\ &=\int-\frac{\sqrt t}{2\sqrt{2t-t^2}}\text dt\\ &=\int-\frac1{2\sqrt{2-t}}\text dt\\ &=\sqrt{2-t}+C. \end{align*}$$ My question is, in the next step, how to set the limits of integration.

Update

By the way, the answer is $2\sqrt2$.

Answer 1

This is quite a long answer...as you already got a great answer. You might peek at it for some real reason why you should adopt that method of periods.

The main problem arises in the range of the arcsine.

First, let's do it the simple trigonometric identity way:

$$I=\int_0^\pi \sqrt{1-\sin 2x}\text dx=\int_0^\pi \sqrt{\sin^2x+\cos^2x-2\sin x\cos x}\text dx=\int_0^\pi \sqrt{(\cos x-\sin x)^2}\text dx=\int_0^\pi |\cos x-\sin x| \text dx$$

Now, for $x\in [0,\pi]$, $(\cos x-\sin x)$ would take positive values (including zero) in the interval $[0,\frac{\pi}{4}]$ and negative values in $(\frac{\pi}{4},\pi]$.

So, we have to split the integral for this two intervals as the mod function would be negative in the second interval. Then, $$\int_0^\pi |\cos x-\sin x|\text dx=\int_0^{\pi/4} (\cos x-\sin x)\text dx+\int_{\pi/4}^\pi -(\cos x-\sin x)\text dx$$

Which would give:

$$I=[\sin x+\cos x]_0^{\pi/4}-[\sin x+\cos x]_{\pi/4}^\pi=2\sqrt2.$$

---

So, we have got our answer now, let's begin with the substitution method.

We let: $$t=1-\sin 2x$$ Since, $x\in [0,\pi]$ so $t\in[0,2]$. Now, $$t=1-\sin 2x \implies x=\frac{1}{2}\arcsin (1-t)\tag{1}$$ Here's the catch: The range of $x$ as implied by the above relation is $[-\frac{\pi}{4},\frac{\pi}{4}]$ but in the integral the original limit requires it to be $[0,\pi]$.

Why this happened?

See, the "principle" range of arcsine is $[\frac{-\pi}{2},\frac{\pi}{2}]$. So, from $eq(1)$, we get that: $$\frac{-\pi}{2}≤2x≤\frac{\pi}{2} \implies \frac{-\pi}{4}≤x≤\frac{\pi}{4} \tag{2}$$

Then, so as to cover the whole range of $x$ i.e. $[0,\pi]$, we have to choose the range of arcsine ourselves and split the integral into the corresponding intervals of range of $x$ which comes form each of the part. Let's decode it:

We have to choose those ranges of arcsine which makes it a function as well as help us extend our range of $x$.

For example, consider the range $[\frac{\pi}{2},\frac{3\pi}{2}]$.We can cover the domain $(-1,1)$ using this range as the sine takes all the values from $1$ to $-1$ exactly one time in this interval.This shows that it makes the arcsine a function.

Now, consider the $eq(1)$ with this range. Then, $x$ would follow: $$\frac{\pi}{2}≤2x≤\frac{3\pi}{2}\implies \frac{\pi}{4}≤x≤\frac{3\pi}{4}\tag{3}$$

Clearly, we have extended the range of $x$ till $3\pi/4$. But we are still less than $\pi$.

Consider another range of arcsine to be $[\frac{3\pi}{2},\frac{5\pi}{2}]$.This again ensures that arsine if a function as before.

Now, the range of $x$ for this range of arcsine would be: $$\frac{3\pi}{4}≤x≤\frac{5\pi}{4}\tag{4}$$

So, we have covered the whole range which we needed for $x$ (actually beyond it).

Now, let's turn to the calculations: $$ x=\frac{1}{2}\arcsin(1-t)\implies \frac{\text dx}{\text dt} = \begin{cases} \frac{-1}{2\sqrt{2t-t^2}} &\quad\text{if}\quad x\in [0,\frac{\pi}{4}]\cup[\frac{3\pi}{4},\frac{5\pi}{4}]\\ \frac{1}{2\sqrt{2t-t^2}} &\quad\text{if}\quad x\in [\frac{\pi}{4},\frac{3\pi}{4}] \\ \end{cases}\tag{5} $$ This is because:[Graphs of arcsine with ranges $[\frac{3\pi}{2},\frac{5\pi}{2}]$(top), $[\frac{\pi}{2},\frac{3\pi}{2}]$(middle) and $[\frac{-\pi}{2},\frac{\pi}{2}]$(bottom)]

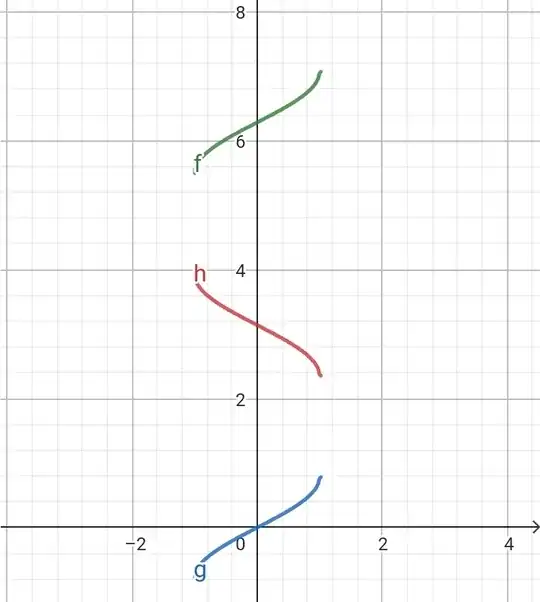
Clearly, the slope of the middle one in negative of other two hence expressed as derivative in $eq(5).$

Now, the splitting: $$I=\int_0^\pi \sqrt{1-\sin 2x}\text dx=\int_0^{\pi/4} \sqrt{1-\sin 2x}\text dx+\int_{\pi/4}^{3\pi/4} \sqrt{1-\sin 2x}\text dx+\int_{3\pi/4}^\pi \sqrt{1-\sin 2x}\text dx$$

By substitution and using $eq(5)$, we get: $$I=\int_1^0-\frac{\sqrt t}{2\sqrt{2t-t^2}}\text dt+\int_0^2\frac{\sqrt t}{2\sqrt{2t-t^2}}\text dt+\int_2^1(-)\frac{\sqrt t}{2\sqrt{2t-t^2}}\text dt=[\sqrt{2-t}]_1^0+[\sqrt{2-t}]_2^0+[\sqrt{2-t}]_2^1=2\sqrt2.$$

The limits of $t$ are set accordingly as the interval of $x$ using the $eq(1)$.

Answer 2

As a hint: It's a periodic function, so you can see $$\int_{0}^{\pi}\sqrt{1-\sin 2x}dx=\int_{0+\frac{\pi}{4}}^{\pi+\frac{\pi}{4}}\sqrt{1-\sin 2x}dx$$ now it has maximum on the interval at $x=\frac{3\pi}{4}$ so you can divide it into two equal integral like below $$\int_{0+\frac{\pi}{4}}^{\pi+\frac{\pi}{4}}\sqrt{1-\sin 2x}dx=2\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}\sqrt{1-\sin 2x}dx$$ and now apply $t$ substitution $$[\frac{\pi}{4},\frac{3\pi}{4}] \\ f(x)=1-\sin 2x \ \text{increasing}\\t=1-\sin 2x \mapsto [0,2] $$

Answer 3

Let's assume that $$I=\int_{0}^{\pi}\sqrt{1-\sin(2x)}dx$$

Here I don't think that one should change the limits.

$\implies I=\int_{0}^{\pi}\sqrt{1-\sin(2x)}dx$

Now $1$ can be written as $\sin^{2}(x)+\cos^{2}(x)$

$\implies I=\int_{0}^{\pi}\sqrt{\sin^{2}(x)+\cos^{2}(x)-\sin(2x)}dx$

$\implies I=\int_{0}^{\pi}\sqrt{\sin^{2}(x)+\cos^{2}(x)-2\sin(x)\cos(x)}dx$

Clearly this is of the form of $\sqrt{(a-b)^{2}}$

$\implies I=\int_{0}^{\pi}\sqrt{(\sin(x)-\cos(x))^{2}}dx$

$\implies I=\int_{0}^{\pi}|\sin(x)-\cos(x)|dx$

Now you have to consider $4$ intervals. Those are $(0,\frac{\pi}{4}),(\frac{\pi}{4},\frac{\pi}{2}),(\frac{\pi}{2},\frac{3\pi}{4}),(\frac{3\pi}{4},\pi)$

$\implies I=\int_{0}^{\frac{\pi}{4}}|\sin(x)-\cos(x)|dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}|\sin(x)-\cos(x)|dx+\int_{\frac{\pi}{2}}^{\frac{3\pi}{4}}|\sin(x)-\cos(x)|dx+\int_{\frac{3\pi}{4}}^{\pi}|\sin(x)-\cos(x)|dx$

Now take into consideration some angles like $30^{°},60^{°},135^{°},150^{°}$ and check whether $(\sin(x)-\cos(x))$ is positive or negative.

If positive then while removing modulus $[\sin(x)-\cos(x)]$ will come and if negative then while removing modulus $[\cos(x)-\sin(x)]$ will come

Finally integrate accordingly. It will be done.

Answer 4

$$\int_{0}^{\pi}\sqrt{1-\sin 2x}dx=\frac12\int_{0}^{2\pi}\sqrt{1-\sin x}dx\overset{x\to \frac\pi2-x}=\frac12\int^{\frac\pi2}_{-\frac{3\pi}2}\sqrt{1-\cos x}dx=\frac12\int^{\pi}_{-\pi}\sqrt{1-\cos x}dx=\int_{0}^{\pi}\sqrt{1-\cos x}dx=\sqrt2\int_{0}^{\pi}\sin(\frac x2)dx=2\sqrt2.$$

Answer 5

As you have already received answers on how to solve the integral by splitting it or by exploiting symmetry to change the bounds, I will share a solution which keeps the bounds same.

Noting that $|x|=x\,\text{sgn}(x)$, we can write the indefinite integral as

$$\begin{align}\int\sqrt{1-\sin2x}\,\mathrm dx&=\text{sgn}(\cos x-\sin x)\int\cos x-\sin x\,\mathrm dx\\&=(\sin x+\cos x)\text{sgn}(\cos x-\sin x)+C\end{align}$$

Now, if we want to directly apply the FTC to compute $\displaystyle \int_0^{2\pi}\sqrt{1-\sin2x}\,\mathrm dx$, we need to ensure its anti-derivative function is continuous in $[0,2\pi]$. You can see why by 'wrongly considering this "anti-derivative"(though it's not actually an anti-derivative, but I'm taking just to explain why anti-derivatives must be continuous) of $2x$:

$$F(x)=\begin{cases}x^2, x<1\\ x^2-1, x\ge 1\end{cases}$$

If we apply the FTC blindly on $F(x)$ to compute $\displaystyle \int_0^12x\mathrm dx$, we get $0$ which is absurd. Hence,

To apply FTC on the anti-derivative of a function to compute its definite integral in a particular interval, the anti-derivative must be continuous in that interval.

The function $f(x)=(\sin x+\cos x)\text{sgn}(\cos x-\sin x)$ is continuous $\forall x\in[0,2\pi]-\left\{\frac\pi4\right\}$. So, we need to redefine $f(x)$ so that it is continuous at $x=\frac\pi4$ if we wish to plug in $x=0$ and $x=2\pi$ directly to evaluate $\displaystyle \int_0^{2\pi}\sqrt{1-\sin2x}\,\mathrm dx$:

$$g(x)=\begin{cases}(\sin x+\cos x)\text{sgn}(\cos x-\sin x)\forall x<\frac\pi4\\ 2\sqrt2+(\sin x+\cos x)\text{sgn}(\cos x-\sin x)\forall x\ge\frac\pi4\end{cases}$$

Hence,

$$\int_0^{2\pi}\sqrt{1-\sin2x}\,\mathrm dx=g(2\pi)-g(0)$$ $$\therefore\boxed{\int_0^{2\pi}\sqrt{1-\sin2x}\,\mathrm dx=2\sqrt2}$$

Answer 6

$$\int\sqrt{1-\sin2x}dx=\int\frac{|\cos2x|}{\sqrt{1+\sin2x}}dx=\operatorname{sgn}(\cos2x)\sqrt{1+\sin2x}+C$$ So, the continuous anti-derivative on $[0,\pi]$ is $$F(x)\begin{cases}\sqrt{1+\sin2x}&\text{if $x\in[0,\frac\pi4]$}\\2\sqrt2+\operatorname{sgn}(\cos2x)\sqrt{1+\sin2x}&\text{if $x\in(\frac\pi4,\pi]$}\end{cases}$$ Hence, $$\int_0^\pi\sqrt{1-\sin2x}dx=F(\pi)-F(0)=2\sqrt2.$$