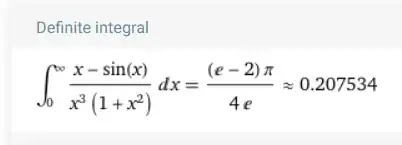Evaluating $\int_{0}^{+\infty}\frac{x-\sin(x)}{x^3(x^2+1)}\,\mathrm dx$ using contour integration and residue calculus

Question

I am trying to evaluate the integral

$$\int_{0}^{+\infty}\frac{x-\sin(x)}{x^3(x^2+1)}\,\mathrm dx.$$

I am thinking of using contour integration, but I do not understand how to do it.

EDIT 1

To begin with, I thought it was necessary to find the poles. $x^3 (x^2 + 1)$.

1. The first factor $x^3$ gives a pole at $x = 0$. Since the degree of $x^3$ is 3, this is a pole of order 3.

2. The second factor $x^2 + 1$ equals zero when: $ x^2 + 1 = 0 \implies x = \pm i. $ These are simple poles because $x^2 + 1$ appears in the denominator to the first power.

Thus, the function $f(x)$ has the following poles:

$x = 0$— a pole of order 3, $x = i$— a simple pole, $x = -i$— a simple pole.

Next, we need to move on to the residue theorem, but since I have found 3 poles, I am stuck.

EDIT 2

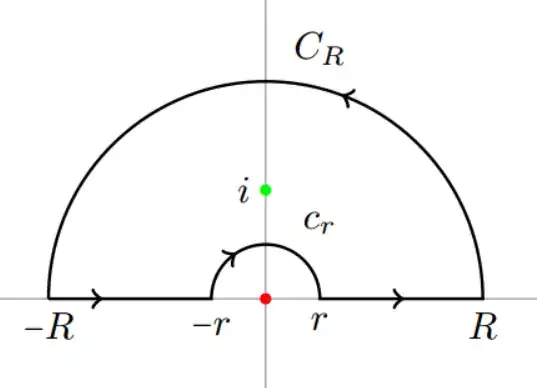
Next, I used the residue theorem to evaluate the integral. Let (f(z)) represent the complex extension of the given function: $$f(z) = \frac{z - \sin(z)}{z^3(z^2 + 1)}.$$

To compute the integral, I considered a contour integral around a semicircular contour in the upper half-plane. This contour includes the poles (z = 0) and (z = i), while avoiding the pole at (z = -i).

The residue theorem states: $$\int_{\text{contour}} f(z) \, \mathrm dz = 2\pi i \sum \text{Res}(f, z_k),$$ where the sum is over all poles inside the contour.

Let’s compute the residues for the poles inside the contour.

Residue at (z = 0) (a pole of order 3):

To find the residue at (z = 0), we use the formula for residues at poles of order 3: $$\text{Res}(f, 0) = \frac{1}{(3-1)!} \lim_{z \to 0} \frac{d^2}{dz^2} \left( z^3 f(z) \right).$$

$$\text{Res}(f, 0) = \frac{i - 2}{2}.$$

Residue at (z = i) (a simple pole):

For a simple pole at (z = i), the residue is: $$\text{Res}(f, i) = \lim_{z \to i} (z - i) f(z).$$

At (z = i), this simplifies to: $$\text{Res}(f, i) = -\frac{e^{-1}}{i}.$$

Residue at (z = -i) (a simple pole):

Similarly, for the simple pole at (z = -i), the residue is: $$\text{Res}(f, -i) = \lim_{z \to -i} (z + i) f(z).$$

At (z = -i), this simplifies to: $$\text{Res}(f, -i) = -\frac{e}{i}.$$

Total Residue and Integral

Summing all residues: $$\text{Total Residue} = \frac{i - 2}{2} - \frac{e^{-1}}{i} - \frac{e}{i}.$$

Using the residue theorem: $$\int_{-\infty}^{+\infty} f(x) \, \mathrm dx = 2\pi i \cdot \text{Total Residue}.$$

Finally, the original integral (over $[0, \infty)$) corresponds to the imaginary part of the result: $$\int_0^{+\infty}\frac{\sin(x)}{x^3(x^2+1)}\,\mathrm dx = \pi \cdot \text{Im}(\text{Total Residue}).$$

$$Im\left(\frac{i-2}{2}+i(e^{-1}+e)\right) = \left(\frac{1}{2}+e^{-1}+e\right)\pi$$

Answer 1

Consider the function $f(z)=\frac{z+ie^{iz}}{z^3(1+z^2)}$. Note that this function has a pole of degree $3$ at $z=0$.

Now consider the Contour $C$ below.

We have:

$$2\pi i\{Res_{z=i} f(z)\}=\int_C f(z)dz\\=\int_r^R \frac{x-\sin x+i\cos x}{x^3(1+x^2)}dx+\int_{C_R} f(z)dz+\int_{-R}^{-r} \frac{x-\sin x+i\cos x}{x^3(1+x^2)}dx+\int_{C_r} f(z)dz.$$

When $R \to \infty $, it's easy to see that $\int_{C_R} f(z)dz \to 0.$ However, we need to be more careful about the Contour $C_r.$ In fact, we have:

$$\int_{C_r} f(z)dz=\int_{C_r} \frac{z+i-z+\frac{i(iz)^2}{2!}+\frac{i(iz)^3}{3!}+\frac{i(iz)^4}{4!}+...}{z^3(1+z^2)}dz.$$ However, note that for $|z| \leq 1$:

$$|\int_{C_r} \frac{\frac{i(iz)^3}{3!}+\frac{i(iz)^4}{4!}+...}{z^3(1+z^2)}dz| \leq (\frac{1}{3!}+\frac{1}{4!}+...) \pi r.$$

Therefore when $r \to 0$,

$$\int_{C_r} \frac{\frac{i(iz)^3}{3!}+\frac{i(iz)^4}{4!}+...}{z^3(1+z^2)}dz \to 0.$$

On the other hand,

$$\int_{C_r} \frac{z+i-z+\frac{i(iz)^2}{2!}}{z^3(1+z^2)}dz=\int_{C_r} \frac{i}{z^3(1+z^2)}dz+\int_{C_r} \frac{-iz^2}{2z^3(1+z^2)}dz.$$

Observe that:

$$\int_{C_r} \frac{i}{z^3(1+z^2)}dz=\int_{C_r} \frac{i}{z^3}dz+\int_{C_r} \frac{iz}{z^2+1}dz-\int_{C_r} \frac{i}{z}dz.$$

It's easy to see that the first integral above is zero. The second one is not dependent on the path when $r \to 0$ (because it would be analytic), so: $$\int_{C_r} \frac{iz}{z^2+1}dz=\int_{-r}^r \frac{ix}{x^2+1}dx=0.$$

And,

$$-\int_{C_r} \frac{i}{z}dz=-\int_{\pi}^0 \frac{ri \times ie^{i\theta}}{re^{i\theta}}d\theta=-\pi.$$

Also,

$$\int_{C_r} \frac{-iz^2}{2z^3(1+z^2)}dz=\int_{\pi}^0\frac{-i \times ire^{i\theta}r^2e^{2i\theta}}{2r^3e^{3i\theta}(1+r^2e^{2i\theta})}d\theta=\int_{\pi}^0\frac{1}{2(1+r^2e^{2i\theta})}d\theta.$$

Therefore, when $r \to 0$, we have: $\int_{C_r} \frac{-iz^2}{2z^3(1+z^2)} \to \frac{-\pi}{2}.$

So, when $r\to 0$,

$$\int_{C_r} f(z)dz \to \frac{-3\pi}{2}.$$

Finally,

$$\int_{-\infty}^{\infty} \frac{x-\sin x}{x^2(1+x^2)}dx=Re \{ 2\pi i \{Res_{z=i}f(z)\}+\frac{3\pi}{2}\}=Re \{2\pi i \frac{i(1+e)}{2e}+\frac{3\pi}{2}\}=\frac{\pi (e-2)}{2e}.$$

---

The answer above is the same as what Wolfram gives: