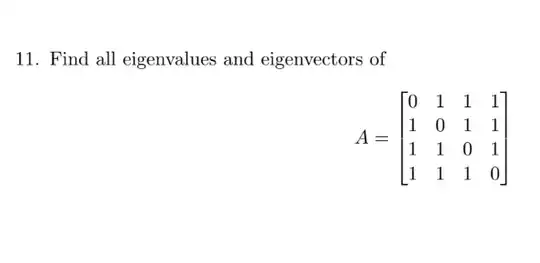0

enter image description here

I'm tackling this practice question, and I doubt it's a plug and chug problem. The matrix is symmetric, and it also looks like it may be related to upper-lower, triangular? Wikipedia calls it a hollow matrix and Wolfram alpha gave a weird answer and none of the steps. I get stuck on the determinant step of finding eigenvalues where the 4x4 matrix looks too big to compute the determinant efficiently.

Any ideas on how to move forward with this?

Edit: turns out row operations with determinant properties are the secret without overcomplicating it too much

Ampersands
  • 33
  • Maybe there is a trick to it, but it is certainly possible (maybe not fun) to get the determinant via cofactor expansion or by reducing to triangular, get the characteristic equation, and then solve using rational root theorem and division. – wzbillings Dec 12 '24 at 18:41
  • 2
    You can just do it, but there's also a trick. Consider $A + I$. – Qiaochu Yuan Dec 12 '24 at 18:49
  • You can easily make two zeroes on the first row by subtracting the fourth row and then expand. – wolfgangmozart12 Dec 12 '24 at 18:57
  • Related: https://math.stackexchange.com/questions/3052997/eigenvalues-of-a-rank-one-update-of-a-matrix – Travis Willse Dec 12 '24 at 19:05
  • The determinant of such a matrix $tI_n-A$ is well known, see this post, for example. It gives immediately that the characteristic polynomial is $(t+1)^3(t-3)$. – Dietrich Burde Dec 12 '24 at 19:23
  • For what it’s worth, it’s pretty easy to guess some eigenvectors. The $i$-th coordinate of $A\vec{v}$ is $\sum_{j\neq i}v_i$, so look at things like $A\langle 1,1,-1,-1\rangle$ and $A\langle 0,2,-1,-1\rangle$. – Steve Kass Dec 12 '24 at 19:23

1 Answers1

1

Hint The form of the matrix suggests considering $A + {\bf 1}_4 = {\bf u}{\bf u}^\top$, where ${\bf u}$ is the $4 \times 1$ vector whose entries are all $1$.

Now:

  1. Compute $\operatorname{rank}(A + {\bf 1}_4)$.
  2. Compute $(A + {\bf 1}_4) {\bf u}$.
  3. Use that $\lambda$ is an eigenvalue of $A$ of multiplicity $m_\lambda$ if and only if $\lambda + \mu$ is an eigenvalue of $A + \mu {\bf 1}_4$ of multiplicity $m_\lambda$.
Travis Willse
  • 108,056