Taylor series has a surprising amount of powers of 10

Question

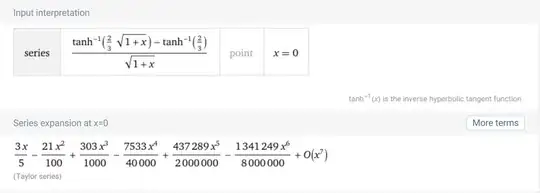
I was messing around with Wolfram Alpha and eventually found the following surprising fact:

\begin{align*}\frac{\tanh^{-1}(\frac23\sqrt{1+x})-\tanh^{-1}(\frac23)}{\sqrt{1+x}}={}&\frac35x-\frac{21}{100}x^2+\frac{303}{1000}x^3-\frac{7\,533}{40\,000}x^4\\&+\frac{437\,289}{2\,000\,000}x^5-\frac{1\,341\,249}{8\,000\,000}x^6+O(x^7)\end{align*}

So many powers of ten! What's happening? Why are they here?

If we call this function $f(x)$, it seems that perhaps $f(10x)$ is the exponential generating function of some integer sequence. That is, it seems that $f(10x)=\sum_{n=0}^\infty c_n\frac{x^n}{n!}$ for some integer sequence $c_n$. Why would this be?

(Even then we should expect the denominator of the sixth term to be $6!\cdot10^6$ rather than the much smaller $8\cdot10^6$.)

It may be useful to know that $$\frac{\tanh^{-1}(\frac23\sqrt{1+x})}{\sqrt{1+x}}=\int_0^1\frac2{1+4t-4xt^2}dt$$ though I don't immediately see how that helps (I see very few $10$s here).

EDIT: The function $f(x)$ also satisfies the differential equation $$2(1+x)f'(x)+f(x)=\frac6{5-4x}$$ with boundary condition $f(0)=0$, if that's useful.

Answer 1

As you've pointed out, the given function $f(x)=\frac{\tanh^{-1}(\frac23\sqrt{1+x})-\tanh^{-1}(\frac23)}{\sqrt{1+x}}$ satisfies the differential equation $2(1+x)(5-4x)f'(x)+(5-4x)f(x)=6$ with $f(0)=0$. We can now consider a power series solution $\sum_{n=0}^\infty a_nx^n$ to the same equation.

For every nonconstant term $a_nx^n$, the LHS of the differential equation becomes $$(-8n-4)a_nx^{n+1}+(2n+5)a_nx^n+10na_nx^{n-1},$$ so the coefficient of $x^n$ in the LHS of the differential equation is $$(-8(n-1)-4)a_{n-1}+(2n+5)a_n+10(n+1)a_{n+1},$$ which must be equal to $0$ for $n\geq 1$. Hence, shifting the indices and rearranging, we have the recursion $$a_n=\frac{-(2n+3)a_{n-1}+(8n-12)a_{n-2}}{10n}.$$ And a $10$ shows up in the denominator! In your case, the starting coefficients are $a_0=0$ and $a_1=\frac 35$. Note that there is a possibility for the numerator to "cancel out" with the $10$ in the denominator (e.g. when going to the $x^6$ term), but holistically speaking this division by $10$ is what leads to the pattern you're noticing.

Generally, the behavior of the power series expansion seems to be closely related to the differential equations the function solves. Differential equations with certain properties (e.g. in this case, a constant term of $10$ in front of the $f'(x)$) can translate those properties recursively into the power series expansion.

Answer 2

Let $f(x) = \sum_{n=0}^{\infty}a_n x^n$ be the Taylor series at $x = 0$. Use your differential equation:

Differentiate it $n$-times to get $$2(1+x)f^{(n+1)}(x) + (1+2n) f^{(n)}(x) = \frac{6\cdot 4^n n!}{(5-4x)^{n+1}}$$

Therefore at $x = 0$: $$2f^{(n+1)}(0)+ (1+2n) f^{(n)}(0) = \frac{6\cdot 4^n n!}{5^{n+1}}$$

By induction it follows for all integers $n\geq 0$ $$(n+1)! \cdot a_{n+1} = f^{(n+1)}(0) = \sum_{k=0}^{n} (-1)^{n-k}\frac{\prod_{r = k+1}^{n} (2r+1)}{2^{n-k}}\cdot\frac{3\cdot 4^k \cdot k!}{5^{k+1}}$$

In particular $$10^{n+1}(n+1)! \cdot a_{n+1} = \sum_{k=0}^{n} (-1)^{n-k}\cdot 2^{k+1}\cdot 5^{n-k}\cdot 3\cdot 4^k \cdot k! \cdot\prod_{r = k+1}^{n} (2r+1) \in \mathbb{Z}$$ Thus, since $c_n = n! 10^n a_n$ for all $n \geq 0$, it is $c_n = 10^n n! a_n \in \mathbb{Z}$ for all $n \geq 1$. Further $c_0 = 0 \in \mathbb{Z}$ and thus $c_n \in \mathbb{Z}$ for all $n \geq 0$.

Answer 3

Comment
Can be re-written: $$ {\ln \left( {\frac {\left( 2\,\sqrt {1+x}+ 3 \right)}{\sqrt{25-20\,x}} } \right) }={\frac{3}{5}}x+{\frac{9}{100}}{x}^{2}+{ \frac{123}{1000}}{x}^{3}+{\frac{1077}{40000}}{x}^{4}+{\frac{100089}{ 2000000}}{x}^{5}+O \left( {x}^{6} \right) $$ Even without the denominator, we have $$ \ln \left( 2\,\sqrt {1+x}+3 \right) =\ln \left( 5 \right) +{\frac{1 }{5}}x-{\frac{7}{100}}{x}^{2}+{\frac{113}{3000}}{x}^{3}-{\frac{971}{ 40000}}{x}^{4}+{\frac{34553}{2000000}}{x}^{5}+O \left( {x}^{6} \right) $$

Answer 4

Here's my own partial progress. Using the integral (rewriting it as $\int_0^1\frac{2/(1+4t)}{1-4xt^2/(1+4t)}\,{\rm d}t$, expanding it as a geometric series, letting $u=1+4t$, and expanding each resulting term using the binomial formula), I have found a formula for the coefficients (different from the one found by psl2Z).

If we write $f(x)=\sum_{n=0}^\infty a_nx^n$, then $$a_n=\frac1{10^n}\cdot\frac1{2^{n+1}}\sum_{\substack{0\le k\le 2n\\ k\ne n}}\left(\left(-1\right)^{k}\binom{2n}k\frac{5^{k}}{k-n}\right).$$ This almost shows that $10^nn!a_n$ is an integer, except for the pesky factor of $\frac1{2^{n+1}}$.

(Nicely, I could almost simply ignore the $-\frac{\tanh^{-1}(\frac23)}{\sqrt{1+x}}$ portion of $f(x)$, since the result was the same as deleting all $u^{-1}$ terms in the transformed integral.)

Answer 5

I would argue that nobody should expect, a priori, any particular constant such as 10 to appear so much more often than others. Here is my earthy, "common sense" approach to this. (I hope I do not come across as condescending or offensive.)

Suppose you prefer to see 11s. Take any series you have that has those 10's and simply change each occurrence of 10 in a term to 11 in its place. The fact that the resulting "new" series may not have a familiar form or, if expressible in some explicit form, not be of current interest? It... is... irrelevant.

Call the resulting function defined by that series S(x). Do this as often as you wish, and then write about how frequently 11's appear in these series for functions like S(x).