A rectangular hyperbola passes through the points A(1, 1), B(1, 5) and C(3, 1). The equation of normal to the hyperbola at A(1, 1) is A:

Question

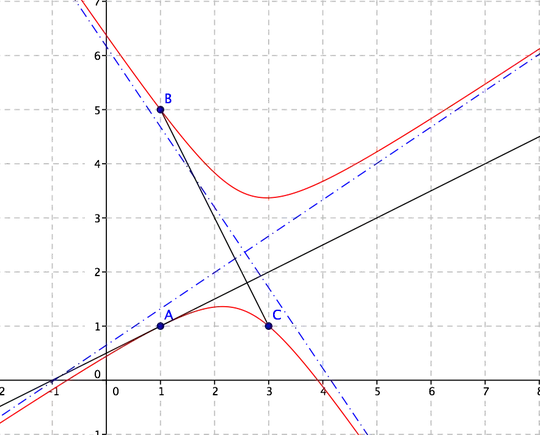
The solution states that the normal at A is parallel to BC. Could someone please explain why that is true. (the answer is 2x+y=3)

Answer 1

First of all, it is obvious that the hyperbola $ABC$ doesn't have its axes or its asymptotes parallel to the coordinate axes (see figure), so that a direct computation of its equation is quite cumbersome.

Fortunately, there is a helpful general result:

If $AB$ and $AC$ are two perpendicular chords of a right hyperbola, then the tangent at $A$ is perpendicular to line $BC$.

I'm giving below an analytical proof, see the EDIT at the end for some other remarks.

As this is a general theorem, for the proof we can choose cartesian axes in a convenient way, for instance coincident with the asymptotes of the right hyperbola, whose equation can then be written as $xy=a$, with $a$ a generic constant.

Let then $A=(x_A,y_A)$ be a generic point on that hyperbola and $m$ be the slope of line $AB$. Point $B$ is the second intersection of that line with the hyperbola and a simple calculation gives: $$ B=\left(-{y_A\over m},-mx_A\right). $$ Let now $C$ be a point on the same hyperbola such that $AC\perp AB$. The slope of line $AC$ is then $-1/m$ and we thus get: $$ C=\left(my_A,{x_A\over m}\right). $$ The slope of line $BC$ is then $$ m_{BC}={x_A\over y_A}, $$ while the slope of the tangent at $A$ is $$ y'(A)=-{y_A\over x_A}. $$ These slopes are then perpendicular, as it was to be proved.

EDIT.

This theorem is a consequence of another well-known property of rectangular hyperbolas:

A triangle $ABC$ inscribed in a rectangular hyperbola has its orthocenter $O$ on that hyperbola

In fact, if $\angle A\to90°$ we have $O\to A$ and altitude $AO$ tends to the tangent at $A$, always remaining perpendicular to $BC$.