0

This question pertains to Example 3.5 of Aluffi's "Algebra: Chapter 0", and is similar to the question asked here: Example 3.5 in Allufi: Chapter 0 (Slice categories). Let $\mathsf{C}$ be some category and $A \in \operatorname{Obj}(\mathsf{C})$. Aluffi defines a new category $\mathsf{C}_A$ where the objects are "all morphisms from any object of $\mathsf C$ to $A$, so (as I understand it), the set

$$ \operatorname{Obj}(\mathsf{C}_A) = \left\{ (Z, f) : Z \in \operatorname{Obj}(\mathsf{C}), f \in \operatorname{Hom}_{\mathsf{C}_A} (Z,A) \right\}. $$ (Edited from $\bigcup_{Z \in \operatorname{Obj}(\mathsf{C})} \mathrm{Hom}_{\mathsf{C}}(Z, A)$ thanks to a comment).
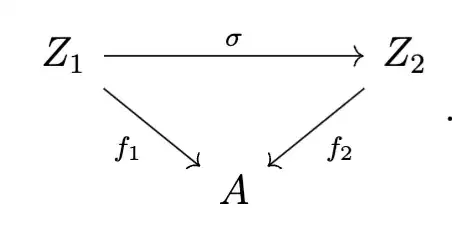
Aluffi then defines morphisms between $f_1, f_2 \in \operatorname{Obj}(\mathsf{C}_A)$ with $f_1 : Z_1 \to A$ and $f_2 : Z_2 \to A$ with $Z_1, Z_2\in \operatorname{Obj}(\mathsf C)$ as the following commutative diagram:

enter image description here

He states that this corresponds precisely to those $\sigma \in \mathrm{Hom}(Z_1, Z_2)$ such that $f_1 = f_2 \circ \sigma$, i.e., such that the diagram commutes.

Now, I am not entirely clear on what the set $\mathrm{Hom}_{\mathsf{C}_A}(f_1, f_2)$ is exactly. Is it the diagram, so a set of objects with a set of morphisms, as Aluffi “defines” it? Or is it those $\sigma$ themselves, so

$$ \operatorname{Hom}_{\mathsf{C}_A}(f_1,f_2) = \left\{ \sigma \in \mathrm{Hom}_{\mathsf{C}}(Z_1, Z_2) : f_1 = f_2 \circ \sigma \right\}? $$ If this right, is it possible to have the actual diagram (whatever that really is, the definition in the book is somewhat unclear to me) as morphisms of some category, as Aluffi's language suggests?

Apologies if this is a somewhat silly question, but I would like to make sure that I don't have a wrong understanding of this (apparently important) example from the beginning!

klonedrekt
  • 171
  • 1
    It doesn't really make a difference: the actual elements of the hom set doesn't matter, and only the relations between them do. So as long as the composition is defined correctly you can view them as either single arrows or entire diagrams. – Trebor Dec 04 '24 at 10:09
  • How do you mean? Doesn't it matter how they are defined in the sense that they have to fulfil the necessary axioms to be a category at all? Do you mean that it doesn't matter if you define them as the set in my question or as the diagrams? My problem is that I can't really work with the diagrams (beyond an intuitive approach), which probably means I don't really know what they are, exactly. – klonedrekt Dec 04 '24 at 10:14
  • For fixed $f_1, f_2$, the set of commutative diagrams like the one you drew, however you define it, should be in bijection with the set you wrote down for $\mathrm{Hom}(f_1, f_2)$, so it doesn't matter. This is structuralism, as opposed to materialism. Your definition of the objects is wrong though: it should be $\sum$, not $\bigcup$. – Naïm Camille Favier Dec 04 '24 at 10:36
  • @NaïmFavier I see, thank you. But why should it be $\sum$ and not $\cup$? How is the sum then defined? – klonedrekt Dec 04 '24 at 10:46
  • $\bigcup$ indicates that you're working in material set theory, where $\mathrm{Hom}$ sets need not be disjoint. $\sum$ is a sigma-type in the sense of dependent type theory, which is a natural home for formalising category theory. You can interpret these as sets of pairs of an object $Z$ of $\mathsf{C}$ and a morphism from $Z$ to $A$. – Naïm Camille Favier Dec 04 '24 at 10:53
  • 1
    @NaïmFavier So $\operatorname{Obj}(\mathsf{C}A) = { (Z, f) : Z \in \operatorname{Obj}(\mathsf{C}), f \in \operatorname{Hom}{\mathsf{C}_A} (Z,A)}$? – klonedrekt Dec 04 '24 at 11:12
  • Yes, for example. – Naïm Camille Favier Dec 04 '24 at 11:21
  • @NaïmFavier I see, this is perhaps why I was having problems trying to show the disjointness of Hom sets in $\mathsf C_A$ with my wrong interpretation of the definition. Thank you very much for your help. – klonedrekt Dec 04 '24 at 11:23
  • @NaïmFavier This should potentially be another question entirely, but I am struggling to show the disjointness axiom; do I have enough information now, or am I potentially still running into the issue described here: https://math.stackexchange.com/questions/98028/verify-this-is-a-category/98358#98358 – klonedrekt Dec 04 '24 at 15:33
  • Oh, I just realised that Aluffi does ask for $\mathrm{Hom}$ sets to be disjoint... that is a very strange convention to take, and it does not hold for the usual encoding of functions as relations unlike he claims (the sets $\emptyset \to A$ and $\emptyset \to B$ are never disjoint). Anyway, this is an unimportant technical detail: if you want them to be disjoint, encode a morphism $f : \mathrm{Hom}(A, B)$ as the triple $(A, B, f)$. – Naïm Camille Favier Dec 04 '24 at 18:11
  • @NaïmFavier Why not an official answer? – Paul Frost Dec 04 '24 at 18:39
  • Concerning the disjointness of $Hom$-sets see my answer to https://math.stackexchange.com/q/4399501/349785. – Paul Frost Dec 04 '24 at 18:43
  • @PaulFrost Thanks, that has cleared up the definition in the book, but I am still struggling with the actual proof, even with encoding $f\in Hom (A,B)$ as the triple $(A,f,B)$ (or in this case $(Z,f)$). Assuming two hom-sets in $C_A$ are not disjoint I get as far as showing that the $Z_1 = Z_3$ and $Z_2 = Z_4$, but the fact that $f_1 = f_2\sigma$ and $f_3 = f_4 \sigma$ doesn't get me anywhere in showing $f_1 = f_3$ and $f_2 = f_4$... am I missing something obvious? – klonedrekt Dec 05 '24 at 14:35
  • 1
    The trick I mentioned works in any category. In this case, you would encode $\sigma$ as $(f_1, f_2, \sigma)$ and then the disjointness of $\mathrm{Hom}$-sets is trivial. – Naïm Camille Favier Dec 05 '24 at 14:44
  • @NaïmFavier now I see, I was only looking at $\sigma$ as a morphism in $\mathsf C$, how silly. Thank you (again)! – klonedrekt Dec 05 '24 at 14:49

1 Answers1

3

Paraphrasing Trebor's and my comments: any correct definition of the set of commutative diagrams such as the one you drew will end up being in bijection with the set you wrote for $\mathrm{Hom}_{\mathsf{C}_A}(f_1, f_2)$, and category theorists like to think up to isomorphism (see structuralism, principle of equivalence), so, yes, that is the correct definition.

Naïm Camille Favier
  • 5,519