How to determine the correct value of a continued fraction when solving the associated equation yields multiple solutions?

Question

I want to calculate the value of this continued fraction:

$$\Large\frac{2}{3-\frac{2}{3-\frac{2}{3-\frac{2}{3-\ddots}}}}$$

So I write:

$$\large x=\frac{2}{3-\frac{2}{3-\frac{2}{3-\frac{2}{3-\ddots}}}}\implies x=\frac{2}{3-x}\implies x_1 = 1,\ x_2 = 2$$

As you saw, we got an equation with two roots, 1 and 2, from the continued fraction. That means the continued fraction is equal to either 1 or 2. But how do we know which one it is?

Answer 1

Short answer (glib)

The expression isn't well-defined, so it's not meaningful to assign a value to infinite continued fraction.

Short answer (sincere)

It's reasonable to assign the value of $1$ to the infinite continued fraction, although there's a caveat, explained below.

Longer answer

We can construct a sequence of rational numbers by beginning with some initial seed $x_0$ and iterating the function $$ f(x) = \frac{2}{3-x}. $$ In other words, we let $x_1 = f(x_0)$, then $x_2 = f(x_1)$, then $x_3 = f(x_2)$, and in general, for any natural number $n$, $$ x_{n+1} = f(x_n). $$ Notice that we can chain these together, so that, e.g., $$ x_3 = f(x_2) = f\bigl(f(x_1)\bigr) = f\Bigl(f\bigl(f(x_0)\bigr)\!\Bigr), $$ which we can also write with superscript notation: $x_3 = f^3(x_0)$, and in general $x_n = f^n(x_0)$. Expressing this in a more intuitive manner, the term $x_n$ is the result of $n$ applications of the function $f$: $$ x_0 \overset{f}{\mapsto} x_1 \overset{f}{\mapsto} x_2 \overset{f}{\mapsto} \cdots \overset{f}{\mapsto} x_n $$

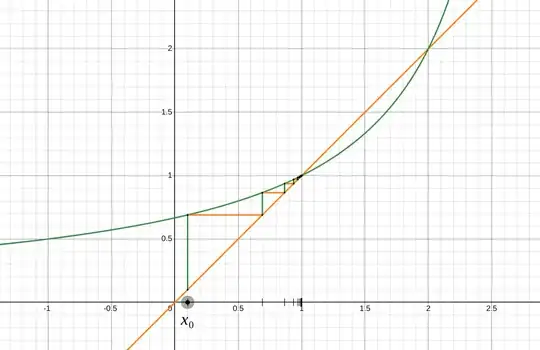
As an example, let's take $x_0 = \color{blue}{0}$. Then, $$ x_1 = f(\color{blue}{0}) = \frac{2}{3 - \color{blue}{0}} = \color{green}{\tfrac{2}{3}}, $$ and $$ x_2 = f\bigl(\color{green}{\tfrac{2}{3}}\bigr) = \frac{2}{3 - \color{green}{\tfrac{2}{3}}} = \color{red}{\tfrac{6}{7}}. $$ This generates the sequence $$ 0, \frac{2}{3}, \frac{6}{7}, \frac{14}{15}, \frac{30}{31}, \frac{62}{63}, \dots $$ You might even recognize a pattern there since both the numerator and denominator are very close to powers of $2$:

$$ x_n = \frac{2^{n+1}-2}{2^{n+1}-1} = 1 - \frac{1}{2^{n+1}-1}$$

It's pretty clear, at least with the seed $x_0 = 0$ that $$ \lim_{n \to \infty} x_n = 1. $$

But what about other seeds? It turns out that for any real number seed with some important exceptions$^\dagger$ the sequence $\{x_0, x_1, x_2, \dots\}$ also converges to $1$. In this interactive graphic, you can drag the seed $x_0$ to various values (or type it in on the left), and watch it generate the sequence of values. Notice how they always find their way to $1$ for this particular function $f$.

---

${}^\dagger$Since $f(2) = 2$, the iterates form the constant sequence $\{2, 2, 2, \dots\}$, clearly with limit $2$. This is special since although its a fixed point, it's unstable, which means that any nearby number, no matter how close, moves away from $2$.

Edited to include the following, thanks to the comment of Federico Poloni: The other exceptions fit into an infinite family. Evidently, $x_0 = 3$ doesn't work because the function $f$ is undefined at $3$, so the sequence of iterates doesn't even get started. But, $x_0 = \tfrac73$ is no good either since in that case $x_1 = f\bigl(\tfrac73\bigr) = 3$ is as far as we can get. In fact, the sequence of negative iterates of $x_0 = 3$ are all problematic: $$ \bigl\{ \dots, f^{-3}(3), f^{-2}(3), f^{-1}(3), f^{-1}(3), 3 \bigr\} = \bigl\{ \dots, \tfrac{31}{15}, \tfrac{15}{7}, \tfrac{7}{3}, 3 \bigr\}. $$ Although there are infinitely many of these bad seeds, they are like dust, discrete points among a continuum of other potential seeds, so in a meaningful sense, they're negligible. For instance, there's zero probability that you would pick any one of them if you picked a random real number seed (uniformly) on some interval of real numbers. Perhaps you can come up with a formula for these numbers, beginning with working out a formula for the inverse $f^{-1}(x)$?

Answer 2

The definition of continued fractions given by Wikipedia implies that in Sammy Black's iterative scheme the seed value $ x_0 = 0 $ should be taken, which leads to the limit value of 1, so the value of your continued fraction is 1. More details below.

According to that Wikipedia page, the value of a continued fraction

$$ b_0+\cfrac{a_1}{b_1+\cfrac{a_2}{b_2+\cfrac{a_3}{b_3+\cdots}}} $$

is the limit (if it exists) of the convergents $A_n/B_n$ for $n→∞$, with

\begin{eqnarray} A_n & = & b_n A_{n-1} + a_n A_{n-2} \\ B_n & = & b_n B_{n-1} + a_n B_{n-2} \end{eqnarray}

for $n ≥ 1$, and

\begin{eqnarray} A_{-1} & = & 1 \\ B_{-1} & = & 0 \\ A_0 & = & b_0 \\ B_0 & = & 1 \end{eqnarray}

In your case, $b_0 = 0$, $a_1 = 2$, $a_n = -2$ for $n ≥ 2$, and $b_n = 3$ for $n ≥ 1$.

Then $$ \dfrac{A_0}{B_0} = \dfrac01 = 0$$ and $$ \dfrac{A_1}{B_1} = \dfrac{b_1 A_0 + a_1 A_{-1}}{b_1 B_0 + a_1 B_{-1}} = \dfrac{3×0 + 2×1}{3×1 + 2×0} = \dfrac23 $$ which is equal to your $f(x)$ if $x = 0$, so $x = 0$ is a good seed value for the iterative scheme.

So your infinite continued fraction is well-defined, because the definition of continued fractions (as given by the Wikipedia article) provides an unambiguous way to construct a sequence of convergents, and that sequence has a well-defined limit in your case. The only infinite continued fractions that are not well-defined are the ones where the sequence of convergents has no well-defined limit, for example because the convergents for even $n$ tend to a different value than the convergents for odd $n$.

Conjecture

The iterative scheme seeks the value of the infinite continued fraction as a solution to the equation $ f(x) = x $. Let's assume that $ X $ is such a solution, so $ f(X) = X $. Then $ f(X + ∆x) ≈ f(X) + f'(X) ∆x $ where $f'(x)$ is the derivative of $f$ with respect to $x$, so if $|f'(X)| > 1$ then the iterative scheme cannot converge on $X$, because each iteration near $X$ brings the candidate $x$ further away from the solution $X$. I conjecture that if $|f'(x)| > 1$ then $x$ cannot be the value of the infinite continued fraction (if the infinite continued fraction has a value).

In your case, $f(x) = 2/(3-x)$ so $f'(x) = 2/(3-x)^2$, $f'(1) = 1/2$, and $f'(2) = 2$, so of the two solutions to $f(x) = x$ that you found, my conjecture says that the one at $x = 2$ cannot be the one that is the value of your infinite continued fraction. That leaves only the solution $x = 1$.