I am trying to understand May's Recognition Principle, specifically its proof.
I will now recall some definition, which can be found in [Geometry of Iterated Loop Space] (or, a concise survey of Maru Sarazola) to make the question a bit more clear.
INTRODUCTION
We are looking at the following operad:
$$\mathcal{C}_k (n)=\textbf{lEmb}\left(\bigsqcup_{j=1}^n I^k, I^k\right)$$
of linear embedding (with 'parallel' sides) and maps
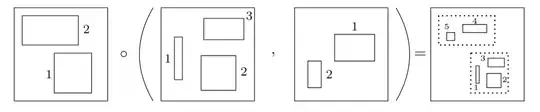
$$\gamma_{n; m_1, \dots, m_n}: \mathcal{C}_k(n) \otimes \mathcal{C}_{k}(m_1) \otimes \dots \otimes \mathcal{C}_{k}(m_n)\rightarrow \mathcal{C}_k (m_1+\dots+m_n)$$
given by nesting as illustrated via a (beautiful) drawing of - again - Sarazola.
Now, we can associate a monad to an operad $\mathcal{O}$, via the following construction (I will only write the image of an object $X$ under the monad) $$OX=\left(\bigsqcup_j \mathcal{O}(j)\times X^j\right)/\sim$$ where quotient is given by the relation $(\sigma_i f, x)\sim (f, s_i x)$ and $(f\sigma, x)\sim (f, \sigma x)$.\
Question
For the proof of the recognition principle we need a particular (weak)h-equivalence: using $C_k$ as the monad associated to the little $k-$cube operad $\mathcal{C}_k$ we have
$$C_k X \stackrel{\text{weak}}{\cong} \Omega^k \Sigma^k X$$
where $\Omega$ and $\Sigma$ are loop space and suspension functors.
My question is then the following.
What is the relationship between the $\mathcal{R}^k$ finite (unordered) configurations labelled in $X$ $$C_k (X)$$ and the image of $X$ with respect to the $C_k$ monad, $C_k X$?
I strongly believe there is a way to directly show a weak h-equiv , motivated by Segal's [Configuration Spaces and Iterated Loop Space] without first going through the h-equiv with the iterated loop of the iterated suspension.
I hope this was clear enough. Everything helps.
Missing Definition and possible answer
For completeness and clarity, I will give the definition I am using for $C_k(X)$.
I will relabel this object as $F_k (X)$ to easily tell it apart from the monad of the little cube operad.
Let us start with $\widetilde{F}_{k, n}$ defined to be
$$\widetilde{F}_{k, n}=\{(x_1, \dots, x_n)\in \mathbb{R}^n| x_i\neq x_j \, \forall i\neq j\}$$
and its quotient
$F_{k, n}=\widetilde{F}_{k, n}/\Sigma_n$
where the symmetric group $\Sigma_n$ is acting (freely and finitely) via permutation of the coordinates.
We can then define and topologize the infinite union
$$F_k = \bigsqcup_n F_{k, n}.$$
This can be generalized by labeling the points by a pointed space $(X, *)$ in the following way:
$$F_k (X)=\left(\bigsqcup_{n} F_{k, n}\times X^n \right)/\sim$$
where the relation $\sim$ identifies points $(c, x)$ and $(c', x')$ if $x$ and $x'$ (thought of as functions from $c$ to $X$ and $c'$ to $X$ respectively) are both constantly $*$ outside the intersection of their domain.
For the possible answer, I think - as mentioned in the comments - theorem $4.8$ (almost?) of May's [Geometry of Iterated Loop Space] completely answers my question in the positive.\
Theorem 4.8: for $1\leq n\leq \infty$ the space $F_{n, j}$ is $\Sigma_j$-equivariantly homotopy equivalent to the operad $\mathcal{C}_j$.
I think I am able to show the homotopy equivalence coherently passes through both the quotients defining the finite configuration labelled by $X$ and the image of $X$ with respect to the monad of the little cube operad.