I just learned about derivatives whose results can be expressed as matrices.
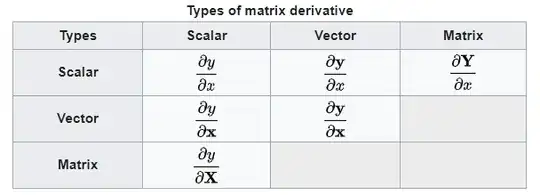
Those types of derivatives are useful. I can find lots of examples in Machine Learning or Optimization Theory. But, I also heard there are some other types of matrix derivatives, such as the matrix-by-matrix derivative, like this one. Basically, to compute this type of derivative, we need to take the differential first, and then vecterize it. It can be viewed as a combination of element-wise scalar derivatives, and can be interpreted using tensor algebra at a higher level seemingly.
What I'm curious about is whether there are specific, meaningful applications of this technique. I tried to search online but found nothing. There are some basic examples, but these meaningless examples are just used to illustrate how to compute the derivatives. For example, the derivate of $F=AX$ where $A$ and $X$ are matrices can be solved as
$$ \begin{gather*} dF = d(AX) = Ad(X)\\ \mathrm{vec}(dF) = \mathrm{vec}(Ad(X)) = (I_n\otimes A)\mathrm{vec}(dX) \end{gather*} $$
But this example doesn't seem to have realistic meaning, which is what I want to find. Could you give me some meaningful examples to illustrate the use and significance of matrix-by-matrix derivative please?