2

I am trying to evaluate the integral: $$ I = \int^{1}_{-1}\frac{1}{\,\sqrt{\,{1 - x^{2}}\,}\,\left(1 + \alpha x^{2}\right)}{\rm d}x $$

using complex analysis.

  • To handle the square root $\sqrt{1 - z^2}$, I place a branch cut for $\sqrt{z}$ along the negative real axis.
  • The contour for this setup consists of:
    • A line segment from $-1$ to $1$ along the real axis.
    • Small semicircles around $z = -1$ and $z = 1$ to avoid singularities, which I believe contribute zero to the integral.
    • Line segments from $-\infty$ to $-1$ and from $1$ to $\infty$.
    • A large semicircle extending to infinity, which I also believe contributes zero to the integral due to the behavior of the integrand at infinity.
      • This can be done using a similar reasoning as for the small semicircle.

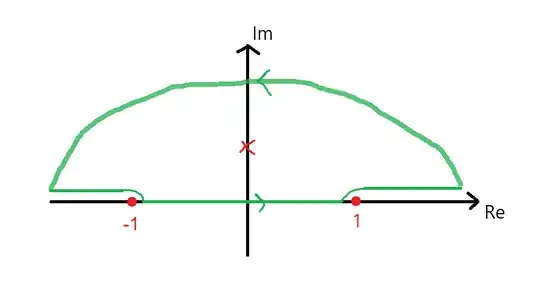
This gives the following image: Considered Integral Path

  • Given this setup, I am unsure how to handle the contributions from the line segments $(-\infty, -1)$ and $(1, \infty)$: Should I evaluate them separately, or can they be related to the original integral on $\left[-1, 1\right]$ ?.
  • I attempted to use the branch cut of $\sqrt{z}$ should be used here, but I tried this and gave no satisfying results.

For now, I just stated the following:

$\oint_{C}{\frac{dz}{\sqrt{1-z^2}(1+\alpha z^2)}} = I_{[-1,1]} + I_{[-\infty,-1]} + I_{[1,\infty]} = 2\pi i \,Res(f,z = \frac{i}{\sqrt{\alpha}})$

Any guidance or hints on how to approach this would be greatly appreciated!

Felix Marin
  • 94,079
EngineerMathlover
  • 321

1 Answers1

1

Hint: Substitute $x=\dfrac y{\sqrt{1+y^2}}\iff y=\dfrac x{\sqrt{1-x^2}}$. The subsequent integral is much simpler using residue calculus; no need to consider residues at infinity.

$$\int_{-1}^1 \frac{dx}{\sqrt{1-x^2}\left(1+\alpha x^2\right)} = \int_{-\infty}^\infty \frac{dy}{1+(1+\alpha)y^2}$$

user170231
  • 25,320