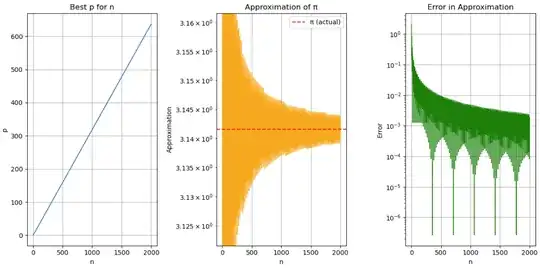
Given $n \in \mathbb{N}$, let $p(n) \in \mathbb{N}$ be such that $n/p(n)$ is the best approximation of $\pi$ (denoted as $\tilde{\pi}_n$). I have two main questions:
- Is the sequence $\{p(n)\}$ a known sequence? If so, is there a closed-form expression for it?
- Can we establish an upper bound for the absolute error of each approximation, $|\pi - \tilde{\pi}_n|$?
Some observations: From numerical computations for $1 \leq n \leq 2000$, we observe the following:
The results suggest that $\max |\pi - \tilde{\pi}_n|$ decays faster than exponentially. However, I am curious if there is a rigorous way to prove this behaviour. I also like the elegant "arches", so I wonder what can be said about those.
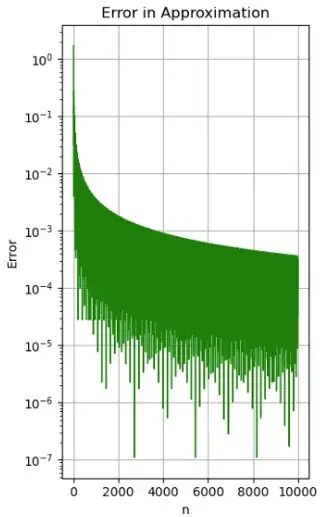
Out of curiosity, this is the error for Euler's number $e$, for $1\leq n\leq 10000$ (the "pillars" seem to have a higher length variance).
In fact, these pillars of irrationality will always occur with some periodicity for any irrational number, never reaching zero. Is this also a definition of an irrational number?