Use Caratheodory to show that if $B^d$ is contained in a convex set $Q$ then $(1-\epsilon)B$ is contained in the convex hull of a finite subset of Q

Question

Consider the following claim:

Claim: Suppose $B^d$ (the unit ball in $\mathbb{R}^d$) is contained in the convex hull of $A$. Then, for every $\epsilon> 0$ there is a finite subset $A_f \subseteq A$ such that $(1-\epsilon)B^d \subseteq \mathrm{conv}(A_f)$.

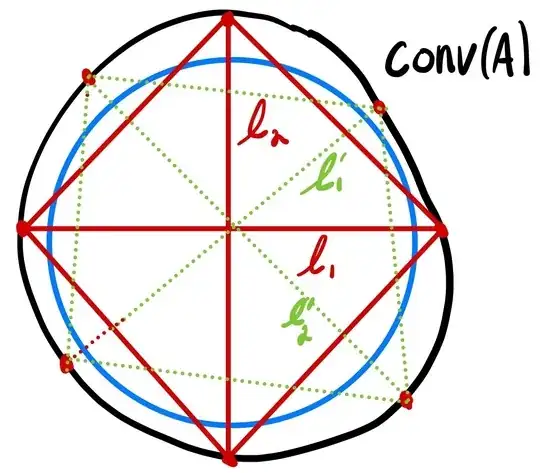
My idea of how to prove this is as follows. Consider $d$ pairwise orthogonal lines through the origin $\ell_1,\dots, \ell_d$. These lines each intersect the boundary of $\mathrm{conv}(A)$ at the points $x_1,y_1$ for $\ell_1$, $x_2,y_2$ for $\ell_2$ etc. Taking the convex hull of $\{x_1,y_1,\dots, x_d,y_d\}$ gives a cross polytope that covers a large (?) portion of the the ball.

By Caratheodory, each $x_i$ and $y_i$ is contained in the convex hull of at most $d+1$ points (actually $d$ points since they're on the boundary) from $A$. My thought is to then rotate these lines finitely many times. After each rotation, add the points from $A$ that convex the intersection points of these lines with the boundary of $A$ to my finite set.

Intuitively it should be that $(1-\epsilon)B^d$ is contained in the convex hull of the set of points obtained after "enough" iterations of this process. However, I have been struggling to write a precise, analytic proof of this.

Any thoughts on how to continue would be greatly appreciated.

UPDATE: By the way it is not too hard to prove this in the plane. Roughly one takes a regular $2n$-gon inscribed in the unit circle. Then the inradius of the $2n$-gon is $\cos\left(\frac{\pi}{2n}\right)$ which tends to $1$ as $n\to \infty$. Thus we can just take the vertices to be those of the $2N$-gon and each of those vertices are contained in the convex hull of at most $d+1$ (so $3$ since we're in the plane) so we can take $6N$ vertices for large enough $N$.

Answer 1

This is an example of something that is geometrically obvious but a pain to prove. Carathéodory is not necessary here. The following is a bit of a grind, hopefully someone will post a more succinct proof.

In the following, $\|\cdot\|$ refers to the Euclidean norm, the $\|\cdot\|_\infty$ norm is also used. I use $\lambda_k$ to refer to convex multipliers, that is, non negative numbers that sum to one.

I am assuming that $B$ is the open unit ball, let $C = \operatorname{co} A$ (the convex hull of $A$) and we are given that $B \subset C$ and $\epsilon>0$. Note that $0 \in C$ and that any point in $C$ can be written as a convex combination of elements of $A$.

Choose $r_1, r_2$ such that $1-\epsilon< r_1 < r_2 < 1$. In particular, the closed convex ball $K =r_2 \overline{B} \subset C$.

Let $R(x) = \{ rx | r \ge 0 \}$ represent the ray through $x$.

Choose some $\delta \in (0, r_2-r_1)$ and suppose that we can find a finite collection $F_\delta \subset \partial K$ that satisfies the following condition: for any $x \neq 0$ there is some subset $x_k \in F_\delta$ (necessarily finite) such that $\|x_i-x_j \| < \delta$ and $\operatorname{co} \{ x_k\}$ intersects $R(x)$. Then, for $y \in \operatorname{co} \{ x_k\} \cap R(x)$ we have $y = \sum_k \lambda_k x_k$ (note that $y$ is a positive multiple of $x$), $\|y-x_1\| \le \sum_k \lambda_k \|x_k-x_1\| < \delta$ and $\|y\| > \|x_1\| - \|y-x_1\| = r_2-\delta>r_1$. In particular, the segment $[0,r_1 {x \over \|x\|}] \subset \operatorname{co} F_\delta$, and since $x \neq 0$ was arbitrary, we see that $r_1 \overline{B} \subset \operatorname{co} F_\delta$ and hence $(1-\epsilon) B \subset \operatorname{co} F_\delta$.

To find such an $F_\delta$, consider the cube $S=[-1,1]^n$, note that $K \subset S$. Pick an integer $m>1$ and let $P = \partial S \cap {1 \over m} \mathbb {Z}^n$, that is, points on the boundary of $S$ that have coordinates that are multiples of ${1 \over m}$. Note that $P$ is finite. It is straightforward to see that for any $x \neq 0$ that $R(x)$ intersects $\partial S$ at some point $\rho x$ and this point is contained in some rectangle whose points lie in $P$ and whose points differ by at most ${1 \over m}$ in each coordinate. That is, $\rho x = \sum_k \lambda_k p_k$ with $p_k \in P$, $\rho>0$ and $\|p_i-p_j\| \le {1 \over m} \sqrt{n}$. Choose $m$ such that ${1 \over m} \sqrt{n} < \delta$. Now let $F_\delta = \{ r_2 {p \over \|p\| } | p \in P \}$, the projection of $P$ onto $K$.

We need to check that $F_\delta$ satisfies the conditions above. Choose $x \neq 0$, then let $\rho x = \sum_k \lambda_k p_k$ with $p_k \in P$ and $\|p_i-p_j\| < \delta$. Since $\rho x = \sum_k (\lambda_k {\|p_k\| \over r_2} )p_k'$, where $p_k'= r_2 {p_k \over \|p_k\|} \in F_\delta$, we see that $R(x)$ intersects $\operatorname{co} \{ p_k' \}_k $. Finally, we note that the projection operator onto a closed convex set is Lipschitz with rank one, we see that $\|p_i'-p_j'\| \le \|p_i-p_j\| < \delta$. (To see the latter, see https://math.stackexchange.com/a/3272185/27978 or a suitably modified version of https://math.stackexchange.com/a/3810235/27978.)