How to calculate the area of a quadrilateral given the (x,y) coordinates of its vertices

Question

This problem is from the 2017 Gauss Contest (Grade 7).

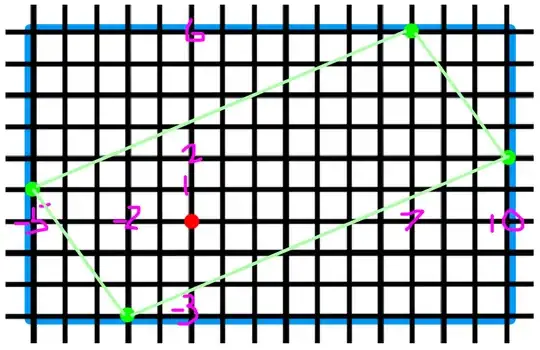
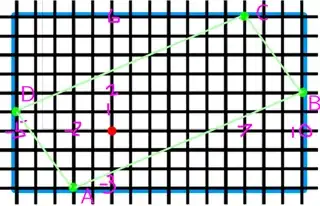
Four vertices of a quadrilateral are located at (7,6), (−5,1), (−2,−3), and (10,2).

What is the area of the quadrilateral in square units?

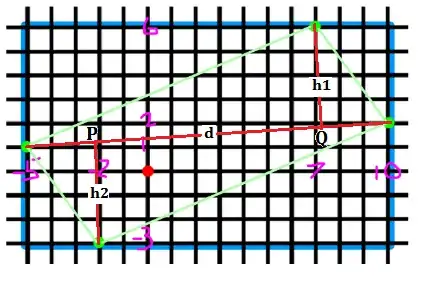
I solved this by graphing the quadrilateral, then drawing a rectangle that encloses the quadrilateral and lastly computing the area of the quadrilateral by the calculation (the area of rectangle minus the total area of the 4 right-angled triangles outside the quadrilateral but inside the rectangle). See my rough sketch below:

My answer of 63 agreed with the official solution. What other ways are there to solve this problem? I don’t care if they are simpler or more complicated than my solution.

Answer 1

Here's a fun way:

Since the points are on a square lattice, use Pick's Theorem and count the integer points on the $b=\color{green}{boundary}$ and on the $i=\color{red}{interior}$

The area is given by a nice formula $$A=\color{red}{i}+\frac{\color{green}{b}}{2}-1$$

Below is the example from wikipedia:

$i=\color{red}{7}$ interior points and $b=\color{green}{8}$ boundary points, so its area is $$A=\color{red}{7}+\frac{\color{green}{8}}{2}-1=10 \color{white}{:)} \text{square units.}$$

Answer 2

One rule that you will love after reading this is the Shoelace Theorem. It allows you to calculate the area of any polygon given that you know all the $(x, y)$ coordinates of the polygon's vertices.

Suppose you have an $n$ sided polygon bounded by the coordinates of its vertices: $$\left(x_1, y_1\right), \left(x_2, y_2\right), \dots, \left(x_n, y_n\right)$$ then, the area $A$ of the polygon is given by the formula: $$A = \frac{\left|\left(x_1y_2 + x_2y_3 + \dots + x_{n-1}y_n + x_ny_1\right) - \left(y_1x_2 + y_2x_3 + \dots + y_{n-1}x_n + y_nx_1\right)\right|}{2}$$ I know the formula may seem a wee bit intimidating, but this isn't called the "Shoelace" Theorem for nothing. Yes, there's a trick to memorizing this formula! Simply create an $(n+2)\times 2$ table as shown below: $$\begin{array}{|c|c|} \hline x & y \\ \hline x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ \vdots & \vdots \\ x_n & y_n \\ x_1 & y_1\\ \hline\end{array}$$ Now, "criss-cross" all $x_i$ with $y_{i+1}$ and then do the same for $y_i$ with $x_{i+1}$. Evaluate the difference of the two sums and finally, divide by $2$ to get your desired area.

Answer 3

The quadrilateral is a parallelogram, so you can use the absolute value of the determinant:

$$ \begin{vmatrix}-5-(-2) && 1-(-3)\\10-(-2) && 2-(-3)\end{vmatrix}$$

Answer 4

This one popped into my head:

$(-5,1)$ and $(10,2)$ form a diagonal across this quadrilateral. It is a parallelogram, but I am not using that here.

The equation of the line that forms this diagonal is $x-15y = -20$

The line parallel through $(-2,3)$ is $x-15y = 43$

The distance of this point from the diagonal is:
$\frac {|43- (-20)|}{\sqrt {15^2 + 1^2}}$

The area of the triangle with these 3 vertices is:

$\frac 12 \frac {|43- (-20)|}{\sqrt {15^2 + 1^2}}\sqrt{15^2 + 1^2} = \frac {63}{2}.$

The line parallel through $(7,6)$ is $x-15y = -83$

The area of the triangle above the diagonal is also $\frac {63}{2}.$

It isn't how I would recommend doing it, but it will work, and it is within the basic algebra curriculum.

Answer 5

HINT:

We can find equations of the diagonal, its length and also lines perpendicular to it (slope negative reciprocal passing through known point) containing altitudes $h1,h2$ with intersections $(P,Q)$.

$$ A= \frac12\cdot d \cdot (h1+h2) $$

Alternately the area of a triangle with three given points can be computed as per determinant of matrix:

$$ \frac12 \cdot \begin{vmatrix}x1 && y1 && 1 \\x2 && y2 && 1 \\ x3 && y3 && 1\end{vmatrix}$$

Two triangle areas one on either side of the diagonal can be computed and summed.

Answer 6

This solutions uses vector math and the cross product. Or if you're feeling fancy you could also use the wedge product from geometric algebra.

Label the vertices as follows:

Since the area is a parallelogram, the area is given by the length of cross product of the side vectors along its diagonals:$$\text{area}=||\vec{AB}\times\vec{AD}\,||$$

The calculation is straightforward. (7,6), (−5,1), (−2,−3), and (10,2). \begin{align} \vec{AB} = \pmatrix{10\\2}-\pmatrix{-2\\-3}=\pmatrix{12\\5}\\ \vec{AD} = \pmatrix{-5\\1}-\pmatrix{-2\\-3}=\pmatrix{-3\\4} \end{align} We now need to promote these vectors to 3D to be able to take the cross product. \begin{align}\vec{AB}\times\vec{AD}&=\pmatrix{12\\5\\0}\times \pmatrix{-3\\4\\0}\\ &=\pmatrix{0\\0\\12\cdot 4-(-3\cdot 4)}\\ &=\pmatrix{0\\0\\63} \end{align} And so the norm of this vector is 63, which is the area.

Equivalently, we can use the wedge product. The computation is identical but we don't need the third dimension. The wedge product has the property that $u\vee v=-v\wedge u$ and $u\wedge u=0$. It also distributes over its argumetns. We calculate the wedge product between $AB$ and $AD$ again: \begin{align} \vec{AB}\wedge \vec{AD}&=(12 e_1+5 e_2)\wedge (-3 e_1+4 e_2)\\ &=12\cdot(-3)\underbrace{e_1\wedge e_1}_0 + 12\cdot 4\, e_1\wedge e_2 + 5\cdot(-3)e_2\wedge e_1 + 5\cdot 4\, \underbrace{e_2\wedge e_2}_0\\ &=12\cdot 4\, e_1\wedge e_2 - 5\cdot(-3)e_1\wedge e_2\\ &=(12\cdot 4 + 5\cdot 3) e_1 \wedge e_2\\ &= 63\, e_1 \wedge e_2 \end{align}