A better method to prove $\lim_{(x,y)\to (0^{+},0^{+})} \frac{x^{3}y}{x^{4}+y^2}=0$

Question

Update: Full solution to this problem

---

---

Note: I know squeeze theorem, polar coordinate,... they can solve the example but they are not generalizable. I put the example in the title so people can relate and understand what is the main topic but it is not the main focus of what I'm asking.

I had trouble understanding the nature of multivariable limits so I tried to find a method to solve as many problems as I could, or even better, I can have a visual of how it works by implementing it on calculators.

I will take the following limit as an example $\lim_{(x,y)\to (0,0)} \frac{x^{3}y}{x^{4}+y^2} $. Firstly, I will narrow the limit $(x,y)\to (0,0)$ down to $(x,y)\to (0^{+},0^{+})$, the complement limits can be achieved either by fixing one variable at $0$ or change of variables get the principle limit $(x,y)\to (0^{+},0^{+})$. Now, I'd like to introduce a "free parameter" $\alpha:=\frac{\ln(1/y)}{\ln(1/x)}>0$ for all $(x,y)\to (0^{+},0^{+})$, equivalently $y=x^\alpha$. We see that $\alpha$ only requires positivity and it is run freely on $(0,+\infty) $ during the limit process, now we substitute $y=x^\alpha$ into the narrowed limit: $$\lim_{(x,y)\to (0^{+},0^{+})} \frac{x^{3}y}{x^{4}+y^2} = \lim_{x\to 0^{+}} \frac{x^{3+\alpha}}{x^4+x^{2\alpha}}= \lim_{x\to 0^{+}} \left(x^{1-\alpha}+x^{-3+\alpha}\right)^{-1}$$ For all $\alpha \in (0,+\infty)$, atleast $1-\alpha$ or $-3+\alpha$ is negative so no matter how we let $\alpha$ run, $x^{1-\alpha}+x^{-3+\alpha}$ will always approach infinity when $x\to 0^{+}$, thus we conclude: $$\lim_{(x,y)\to (0^{+},0^{+})} \frac{x^{3}y}{x^{4}+y^2}=0$$ The first example is done here.
I will also provide how I generalize the method, for example: $$\lim_{(x,y,z)\to (0^{+},0^{+},0^{+})}\frac{xy+z}{x^2+y^2+z^2}\overset{(y=x^{\alpha},z=x^{\beta})}{=} \lim_{x\to 0^{+}} \left((x^{1-\alpha}+x^{\alpha-1}+x^{2\beta-\alpha-1})^{-1}+(x^{2-\beta}+x^{2\alpha-\beta}+x^{\beta})^{-1}\right)$$ There are 2 parameters, things are not obvious for human but I think Linear Programming could handle them.
Question:
How good/correct this method is? In what cases it can go wrong?
I assume that the indeterminate limit in question has this form: $$\lim_{(x_1,...,x_n)\to(0^{+},...,0^{+})} \frac{\sum_{i}c_{1i}x_{1}^{a_{i1}}...x_{n}^{a_{in}}}{\sum_{j}c_{2j}x_{1}^{b_{j1}}...x_{n}^{b_{jn}}}$$ where $c_{1i},c_{2j}>0$ and $a_{ik},b_{jk}\in \mathbb{R}$

---

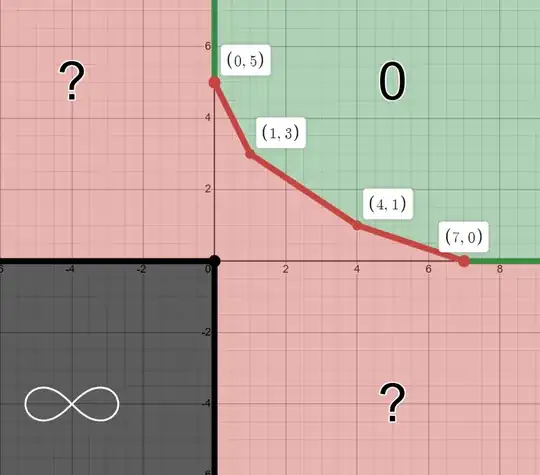
Extension I took one step furthur into the investigation and suprisingly, this is what I found: (below is an example but I think it is enough for you to see what's going on):
$$L=\lim_{(x,y)\to (0^{+},0^{+})}\frac{x^{a}y^{b}}{x^{7}+x^{4}y+xy^{3}+y^{5}}$$ The image below is graph of limit with respect to $(a,b)$ in $\mathbb{R}^{2}$
Note that colors of edges and points are counted
(green=limit is $0$; red=essentially undecidable; black=limit is $+\infty$)

The logic seems to apply consistently with computation result, my method agrees too.
So "Polytopes solve limits"?

I will leave this as an unproven conjecture (the generalized in n dimensions) for anyone who is interested. Any ideas are appreciated.

Answer 1

Your method works because you are only interested in limits in $(0^+,\ldots,0^+)$ so you have positive variables. You must be careful however, about the fact that the variables $\alpha$ and $\beta$ you introduce may vary, which may affect the limit. I think the best way to write it is to work directly with the logarithms of you variables. In this way, your conjecture can be proven. Consider a function of the form, $$ F(x_1,\ldots,x_n) = \sum_{k \in S} F_kx^k, $$ where $S$ is a finite subset of $\mathbb{R}^n$ and for all $k = (k_1,\ldots,k_n) \in \mathbb{R}^n$, $x^k = x_1^{k_1}\cdots x_n^{k_n}$. Also assume that the $F_k$ are positive and that each $x_i$ appears at least once, so when all the $x_i$ are positive, $F(x_1,\ldots,x_n) > 0$. In your example, $S = \{(0,5),(1,3),(4,1),(7,0)\}$ and $F_{(0,5)} = F_{(1,3)} = F_{(4,1)} = F_{(7,0)} = 1$.

We are looking for the real vectors $a \in \mathbb{R}^n$ such that, $$ \lim_{x \rightarrow (0^+,\ldots,0^+)} \frac{x^a}{F(x)} = 0. $$ Your conjecture is that this is equivalent to $a$ belongs to some unbounded convex polygon depending on $S$ that we will define later (see the comment of @MathFont).

Introduce $y_i = -\ln(x_i)$ which diverges toward $+\infty$ when $x_i \rightarrow 0^+$. For all $k \in \mathbb{R}_+^n$, $$ x^k = x_1^{k_1}\cdots x_n^{k_n} = \exp(-y_1k_1 - \cdots - y_nk_n) = \exp(-\left<y,k\right>). $$ Now define the following open convex polygon, $$ P = \{a \in \mathbb{R}^n|\exists p \in \mathrm{Conv}(S), a - p \textrm{ only has postive coefficients}\} $$ I don't know if there is a "cleaner" way to define it, because it is not exactly a Newton polygon. Here, $\mathrm{Conv}(S)$ is the convex hull of $S$. In your example, $P$ is the interior of the green area. We can show the following statement,

Claim : $$ a \in P \Longrightarrow \lim_{x \rightarrow (0^+,\ldots,0^+)} \frac{x^a}{F(x)} = 0 \Longrightarrow \frac{x^a}{F(x)} \textrm{ is bounded around } (0^+,\ldots,0^+) \Longrightarrow a \in \overline{P}. $$ I let you figure this out the cases whether or not we have convergence toward $0$ when $a \in \partial P$.

---

Direct sens :

To prove it, if $p$ is a point of the convex hull of $S$, we may write it as, $$ p = \sum_{k \in S} t_kk, $$ where the $t_k$ are non-negative and their sum equals $1$. Let $C > 0$ be a positive real number such that for all $k \in S$, $F_k \geqslant Ct_k$. If $x \in \mathbb{R}_+^{*n}$, if $y = (-\ln(x_1),\ldots,-\ln(x_n))$, \begin{align*} \frac{x^a}{F(x)} & = \frac{\exp(-\left<y,a\right>)}{\sum_{k \in S} F_k\exp(-\left<y,k\right>)}\\ & \leqslant \frac{\exp(-\left<y,a\right>)}{\sum_{k \in S} Ct_k\exp(-\left<y,k\right>)}\\ & \leqslant \frac{\exp(-\left<y,a\right>)}{C\sum_{k \in S} \exp(-\left<y,t_kk\right>)} \textrm{ by Jensen's inequality,}\\ & = \frac{1}{C}\exp\left(-\left<y,a - \sum_{k \in S} t_kk\right>\right)\\ & = \frac{1}{C}\exp(-\left<y,a - p\right>). \end{align*} $C$ depends on $p$ but not on $y$. If $a \in P$, we can choose $p$ such that all the coefficients of $a - p$ are positive, so, $$ \left<y,a - p\right> \rightarrow +\infty, $$ when $y \rightarrow (+\infty,\ldots,+\infty)$ thus $\frac{x^a}{F(x)} \rightarrow 0$ when $x \rightarrow (0^+,\ldots,0^+)$.

---

Reciprocal :

For the reciprocal, let $Q$ be the set of all $a$ such that $\frac{x^a}{F(x)}$ is bounded near $(0^+,\ldots,0^+)$. If $(a,b) \in Q^2$ and $0 \leqslant t \leqslant 1$, then, by Jensen's inequality, $$ \frac{x^{ta + (1 - t)b}}{F(x)} \leqslant \frac{tx^a + (1 - t)x^b}{F(x)} = \mathrm{O}(1), $$ so $ta + (1 - t)b \in Q$. It proves that $Q$ is convex. Moreover, if $q \in Q$ and $a$ is such that $a - q$ only has non-negative coefficients, $$ \frac{x^a}{F(x)} = x^{a - q}\frac{x^q}{F(x)} = \mathrm{O}(1), $$ so $a \in Q$. If $S \subset Q$, then $\mathrm{Conv}(S) \subset Q$ by convexity of $Q$ so, $$ \overline{P} = \{a \in \mathbb{R}^n|\exists p \in \mathrm{Conv}(S), a - p \textrm{ only has non-negative coefficients}\} \subset Q. $$ It show that it is enough to prove that $S \subset Q$. And if $a \in S$, $$ \frac{x^a}{F(x)} = \frac{x^a}{\sum_{k \in S} F_kx^k} \leqslant \frac{1}{F_a}, $$ so, as wanted, $S \subset Q$. It proves the reciprocal.

---

You might be interested in tropical geometry and amoebas, where this kind of reasoning with real convex geometry frequently appears. I hope the proof was clear.

Answer 2

I think we may as well try squeeze theorem here.

Since we are taking limit for $(x,y)$ to tend to $(0^+, 0^+)$, we can assume $x > 0, y>0$.

Then for any $a,b \in \mathbb{R}$, we have the inequality

$$a^2 + b^2 \geq 2ab$$

and this implies

$$\forall x > 0, \forall y > 0, x^3 y = x \cdot x^2 \cdot y \leq \frac{x}{2} (x^4 + y^2)$$

So we have

$$0 < \frac{x^3 y }{x^4 + y^2} \leq \frac{x}{2} \frac{x^4 + y^2}{x^4 + y^2} = \frac{x}{2}$$

Then by squeeze theorem, since

$$\lim_{(x,y) \rightarrow (0^+,0^+)} 0 = \lim_{(x,y) \rightarrow (0^+,0^+)} \frac{x}{2} = 0 $$

we can conclude that

$$\lim_{(x,y) \rightarrow (0^+,0^+)} \frac{x^3 y }{x^4 + y^2} = 0$$