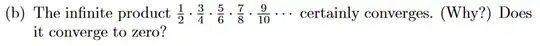(No this is not a duplicate question, ive seen the proofs on other MSE posts and i accept them but i'm trying to understand why my proof is incorrect)
This is a question presented in Abbott's Understanding Analysis. I've somehow proven that it both does and does not converge to 0. Looking online, it seems that converging to 0 is the correct answer but i still don't know what's wrong with my other proof. I will use $\prod a_n$ to denote the partial product up to m.
- We have $\prod \frac{2n+1}{2n}$ converges (proven earlier in the book). Lets call the limit L, which is clearly greater than 1.
Let $\prod \frac{2n-1}{2n} \to K$ be the limit of the sequence given in the question.
Then $\prod \frac{2n-1}{2n+1}$ = $\prod \frac{2n-1}{2n} \frac{2n}{2n+1}$ = $\prod \frac{2n-1}{2n} \prod \frac{2n}{2n+1}$ = $\prod \frac{2n-1}{2n} \frac{1}{\prod \frac{2n+1}{2n}}$which converges to K/L.
$\prod \frac{2n-1}{2n+1}$ converges to 0 by cancelling terms. So K/L = 0 so K = 0.
- Suppose it converges to 0. So $\sqrt[m]{\prod a_n} \to 0$ It is clear that $\prod 2a_n = 2^m\prod a_n$ does not converge as the terms converge to 2.
For all $\epsilon$ there exists M such that for all m>M $\sqrt[m]{\prod a_n} < \epsilon$ so $\prod a_n <\epsilon^m$.
Set $\epsilon = 1/3$. Thus $\prod a_n <1/3^m$. So $2^m \prod a_n <2/3^m$. So $2^m \prod a_n$ converges which is absurd. So $\prod \frac{2n-1}{2n}$ does not converge to 0.