Yesterday, I posted this question about Rock Paper Scissors: Mathematics of Rock Paper Scissors game
I recently thought of the following questions:
Suppose there are 1000 players at the start. At the start of the first round, pairs of players are made Each pair of players plays only 1 game (best of 3). The winners move to the next round, the loser is instantly eliminated.
- Q1: On average, how many ties can we expect in this game? Can we know the variance?
- Q2: On average, at what round and at which turn will the 1000th tie happen? Can we know the variance?
I was not sure how to analyze these problems, so I tried to simulate them:
Can someone please show me how to mathematically answer these questions?
Here is the computer code (R) used for these simulations:
library(ggplot2)
library(dplyr)
library(viridis)
library(gridExtra)
library(tidyr)
analyze_rps_tournament <- function(n_players, n_sims = 1000, target_tie = 250, n_trajectories = 100) {
simulate_single_match <- function() {
games <- 0
ties <- 0
repeat {
games <- games + 1
choices <- sample(1:3, 2, replace = TRUE)
if (choices[1] == choices[2]) {
ties <- ties + 1
} else {
break
}
}
return(list(games = games, ties = ties))
}
simulate_tournament <- function(n_players) {
if (n_players < 2 || n_players %% 2 != 0) {
stop("Number of players must be even and at least 2")
}
players <- 1:n_players
round_num <- 1
total_games <- 0
total_ties <- 0
games_by_round <- list()
ties_by_round <- list()
while (length(players) > 1) {
round_games <- 0
round_ties <- 0
winners <- c()
for (i in seq(1, length(players), 2)) {
match_result <- simulate_single_match()
round_games <- round_games + match_result<span class="math-container">$games
round_ties <- round_ties + match_result$</span>ties
winners <- c(winners, players[i + sample(0:1, 1)])
}
games_by_round[[round_num]] <- round_games
ties_by_round[[round_num]] <- round_ties
total_games <- total_games + round_games
total_ties <- total_ties + round_ties
players <- winners
round_num <- round_num + 1
}
return(list(
games_by_round = games_by_round,
ties_by_round = ties_by_round,
total_games = total_games,
total_ties = total_ties,
n_rounds = round_num - 1
))
}
cat("Running general tournament statistics...\n")
results <- list()
for(i in 1:n_sims) {
if(i %% 100 == 0) cat("Running simulation", i, "of", n_sims, "\n")
results[[i]] <- simulate_tournament(n_players)
}
games_df <- data.frame(
round = rep(1:results[[1]]<span class="math-container">$n_rounds, n_sims),
games = unlist(lapply(results, function(x) unlist(x$</span>games_by_round))),
simulation = rep(1:n_sims, each = results[[1]]$n_rounds)
)
ties_df <- data.frame(
round = rep(1:results[[1]]<span class="math-container">$n_rounds, n_sims),
ties = unlist(lapply(results, function(x) unlist(x$</span>ties_by_round))),
simulation = rep(1:n_sims, each = results[[1]]$n_rounds)
)
game_trajectories <- games_df %>%
group_by(simulation) %>%
mutate(cum_games = cumsum(games)) %>%
ungroup()
tie_trajectories <- ties_df %>%
group_by(simulation) %>%
mutate(cum_ties = cumsum(ties)) %>%
ungroup()
total_ties <- sapply(results, function(x) x<span class="math-container">$total_ties)
total_games <- sapply(results, function(x) x$</span>total_games)
ties_mean <- mean(total_ties)
ties_sd <- sd(total_ties)
games_mean <- mean(total_games)
games_sd <- sd(total_games)
cat("\nTheoretical Expectations:\n")
cat(sprintf("Expected games per match: 1.5\n"))
cat(sprintf("Expected total games: %.1f\n", (n_players - 1) * 1.5))
cat(sprintf("Expected total ties: %.1f\n", (n_players - 1) * 0.5))
cat("\nSimulation Results:\n")
cat(sprintf("Mean total games: %.1f ± %.1f\n", games_mean, games_sd))
cat(sprintf("Mean total ties: %.1f ± %.1f\n", ties_mean, ties_sd))
sampled_sims <- sample(unique(game_trajectories$simulation), n_trajectories)
sim_subtitle <- sprintf("%d Players, %d Simulations", n_players, n_sims)
common_theme <- theme_minimal() +
theme(axis.text.x = element_text(angle = 0),
panel.grid.minor = element_blank())
p1 <- ggplot() +
geom_line(data = subset(tie_trajectories, simulation %in% sampled_sims),
aes(x = factor(round), y = cum_ties, group = simulation),
color = "#440154FF", alpha = 0.1) +
stat_summary(data = tie_trajectories,
aes(x = factor(round), y = cum_ties),
fun = mean, geom = "line",
color = "red", size = 1, group = 1) +
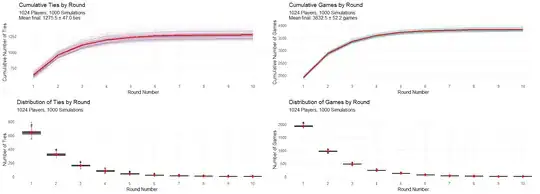
labs(title = "Cumulative Ties by Round",
subtitle = sprintf("%s\nMean final: %.1f ± %.1f ties",
sim_subtitle, ties_mean, ties_sd),
x = "Round Number",
y = "Cumulative Number of Ties") +
common_theme
p2 <- ggplot() +
geom_line(data = subset(game_trajectories, simulation %in% sampled_sims),
aes(x = factor(round), y = cum_games, group = simulation),
color = "#238A8DFF", alpha = 0.1) +
stat_summary(data = game_trajectories,
aes(x = factor(round), y = cum_games),
fun = mean, geom = "line",
color = "red", size = 1, group = 1) +
labs(title = "Cumulative Games by Round",
subtitle = sprintf("%s\nMean final: %.1f ± %.1f games",
sim_subtitle, games_mean, games_sd),
x = "Round Number",
y = "Cumulative Number of Games") +
common_theme
p3 <- ggplot(ties_df, aes(x = factor(round), y = ties)) +
geom_boxplot(fill = "#440154FF", alpha = 0.6, outlier.alpha = 0.3) +
stat_summary(fun = mean, geom = "point", shape = 18, size = 3, color = "red") +
labs(title = "Distribution of Ties by Round",
subtitle = sprintf("%s\nRounds 1-%d, â—† marks mean",
sim_subtitle, results[[1]]$n_rounds),
x = "Round Number",
y = "Number of Ties") +
common_theme
p4 <- ggplot(games_df, aes(x = factor(round), y = games)) +
geom_boxplot(fill = "#238A8DFF", alpha = 0.6, outlier.alpha = 0.3) +
stat_summary(fun = mean, geom = "point", shape = 18, size = 3, color = "red") +
labs(title = "Distribution of Games by Round",
subtitle = sprintf("%s\nRounds 1-%d, â—† marks mean",
sim_subtitle, results[[1]]$n_rounds),
x = "Round Number",
y = "Number of Games") +
common_theme
grid.arrange(p1, p2, p3, p4, ncol = 2)
cat(sprintf("\nAnalyzing location of %dth tie...\n", target_tie))
tie_locations <- data.frame(
simulation = integer(),
round = integer(),
game = integer()
)
for(i in 1:n_sims) {
if(i %% 100 == 0) cat("Running simulation", i, "of", n_sims, "\n")
players <- 1:n_players
round_num <- 1
total_ties <- 0
game_num <- 0
found_target <- FALSE
while(length(players) > 1 && !found_target) {
n_matches <- length(players) / 2
for(match in 1:n_matches) {
repeat {
game_num <- game_num + 1
choices <- sample(1:3, 2, replace = TRUE)
if(choices[1] == choices[2]) {
total_ties <- total_ties + 1
if(total_ties == target_tie) {
tie_locations <- rbind(tie_locations,
data.frame(
simulation = i,
round = round_num,
game = game_num
)
)
found_target <- TRUE
break
}
} else {
break
}
}
if(found_target) break
}
players <- players[seq(1, length(players), 2)]
round_num <- round_num + 1
}
}
if(nrow(tie_locations) > 0) {
avg_game <- mean(tie_locations<span class="math-container">$game)
avg_round <- mean(tie_locations$</span>round)
sd_game <- sd(tie_locations<span class="math-container">$game)
sd_round <- sd(tie_locations$</span>round)
cat(sprintf("\nStatistics for %dth Tie:\n", target_tie))
cat(sprintf("Average Game: %.1f (SD: %.1f)\n", avg_game, sd_game))
cat(sprintf("Average Round: %.1f (SD: %.1f)\n", avg_round, sd_round))
heatmap_data <- tie_locations %>%
group_by(round, game) %>%
summarise(count = n(), .groups = 'drop') %>%
mutate(percentage = count / n_sims * 100)
game_breaks <- pretty(heatmap_data$game)
p_heatmap <- ggplot(heatmap_data, aes(x = game, y = factor(round), fill = percentage)) +
geom_tile() +
scale_fill_viridis_c(
name = "% of\nSimulations",
option = "viridis" # Using viridis color scheme (blue-green-yellow)
) +
scale_x_continuous(
breaks = game_breaks,
labels = game_breaks
) +
labs(
title = sprintf("Location of %dth Tie in Tournament", target_tie),
subtitle = sprintf("%d Players, %d Simulations\nMean Game: %.1f (±%.1f), Mean Round: %.1f (±%.1f)",
n_players, n_sims, avg_game, sd_game, avg_round, sd_round),
x = "Game Number",
y = "Round Number"
) +
theme_minimal() +
theme(
panel.grid = element_blank(),
axis.text.x = element_text(angle = 45, hjust = 1),
legend.position = "right",
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5)
)
print(p_heatmap)
} else {
cat(sprintf("No simulations reached %d ties\n", target_tie))
}
}
set.seed(42)
analyze_rps_tournament(
n_players = 1000,
n_sims = 1000,
target_tie = 250,
n_trajectories = 100
)