Is there a general approximation scheme for integral like $\int_{-\infty}^\infty f(x)/(x^2+a^2) dx$

Question

I posted a question concerning the integration of:

$$ I(a)=8a\int_{-\infty}^{\infty} \frac{K^2}{(4K^2+a^2\pi^2)\sinh^2(K)}dK $$

Numerous nice answers found the result to be:

$$I(a)=-4-4a+2a^2\psi^{(1)}(a/2)$$

with $\psi^{(1)}$ the trigamma function.

The computation of the integral is relatively convoluted and I was wondering if there was a way to obtain directly (and relatively easily) an expansion in small $a$ of the integral form of $I(a)$ that would lead to the same expansion of the final result of $I(a)$? More generally perhaps, I often find hard to find approximate results for integrals of the form: $\int_{-\infty}^\infty f(x)/(x^2+a^2) dx$ for which we cannot simply expand $(x^2+a^2)^{-1}$ in small $a$ and where changes of variable in $x\to ax$ is not too useful.

---

As an example, we can perform the following change of variable:

$$I(a)=8a\int_{-\infty}^{\infty} \frac{K^2}{(4K^2+a^2\pi^2)\sinh^2(K)}dK=8a^2\int_{-\infty}^\infty \dfrac{k^2}{4k^2+\pi^2}\dfrac{1}{\sinh^2(ak)}dk$$

Then expand $\sinh^2(x)=x^2+\frac{x^4}{3}+\mathcal{O}(x^6)$ and integrate to obtain:

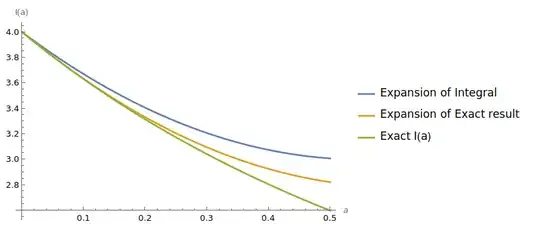
$$I(a)=4-\dfrac{2\pi}{\sqrt{3}}a+\frac{\pi^2}{3}a^2+\mathcal{O}(a^3)$$

Which is different and really less accurate than the expansion of the exact form of $I(a)$:

$$I(a)=-4-4a+2a^2\psi^{(1)}(a/2)=4-4a+\dfrac{\pi^2}{3}a^2+\mathcal{O}(a^3)$$

I also tried using Padé Approximant but it's not helping too much and in any case, approximations beyond the 4th order become really tricky due to the complicated integrals.

Any help toward a solution is appreciated!

Answer 1

We cannot use series expansion around $a=0$ since this would lead to divergent integrals.

However, no problem for large values of $a$ $$ \frac{8a K^2}{(4K^2+a^2\pi^2)\sinh^2(K)}=\sum_{n=0}^\infty (-1)^n\,\frac {2^{2 n+3} } {\pi ^{2 (n+1)} a^{2 n+1} }\,\frac{K^{2(n+1)}}{\sinh^2(K)} $$ For general $n$, I did not find the explicit result of $$J_n=\int_{-\infty}^{+\infty}\frac{K^{2(n+1)}}{\sinh^2(K)}\,dK $$ but it does not make any problem for specific $n$.

As a result, for large $n$

$$I(a)=\frac 83 \sum_{n=0}^\infty (-1)^n \frac{\alpha_n}{\beta_n}\,a^{-(2n+1)}$$ where the $\alpha_n$ and $\beta_n$ correspond to sequences $A345365$ and $A177735$ in $OEIS$ where their explicit formulae are given.

For the first terms, we have $$I(a)=\frac{8}{3 a}-\frac{32}{15 a^3}+\frac{128}{21 a^5}-\frac{512}{15 a^7}+\frac{10240}{33 a^9}-\frac{5660672}{1365 a^{11}}+O\left(\frac{1}{a^{13}}\right)$$ which is the series expansion of

$$2 a^2 \psi ^{(1)}\left(\frac{a}{2}\right)-4 a-4$$