Sum of two uniform random variable how to find integration limits

Question

I'm trying to solve a problem that asks me to find me the p.d.f of $Y = X_1 + X_2$, where both $X_1$ and $X_2$ are uniformly distributed over $[0,1]$. In order to do that I need to solve this:

$$ \int_{-\infty}^{\infty} f_{X_1}(x) f_{X_2}(y-x) d x $$

but I have trouble understanding how to find the limits of integration.

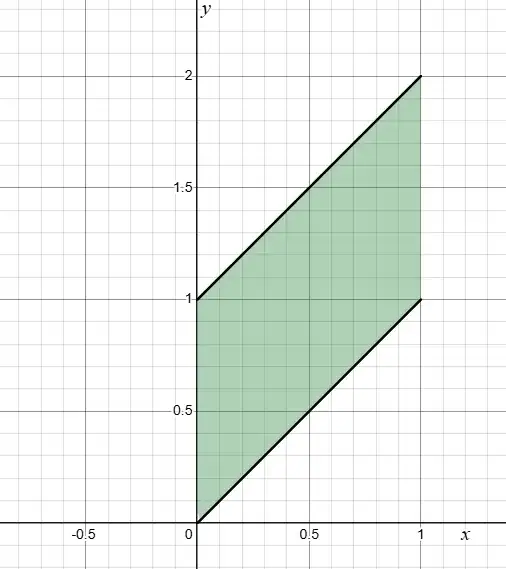
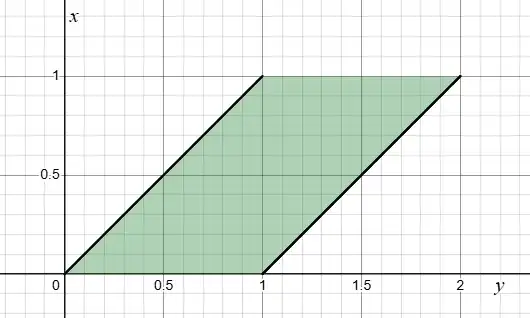
I know that $Y \in [0,2]$ and if I let $X_1 = x$, then $X_2 = y-x$. Then I think I have to solve two cases (but not sure why).

Case I: $0 \leq y \leq 1$ I think that I have to solve $0 \leq x \leq 1$ and $0 \leq y-x \leq 1$

Case II: $1 \leq y \leq 2$.

It feels like there should be an easy way to do this, but I'm missing something essential that I need to proceed. I really don't understand how to approach finding the limits. I should note that I'm not great at working with inequalities, so that might be the reason why I am stuck.

Thankful for any advice.

EDIT

$X_1$ and $X_2$ are i.i.d.

Answer 1

Here another more simple and intuitive solution with a drawing. As you mentioned, we have $Y = X_1 + X_2$ and $X = X_1$. We original know $x_1,x_2 \in (0,1)^2$, then \begin{align*} 0 & < x_1 < 1 \\ x_1 & < x_1 + x_2 < 1+x_1 \\ 0 & < x_1 < x_1 + x_2 < 1+ x_1 \\ 0 & < x < y < 1+ x \end{align*} with $x_1 = x \in (0,1)$, this region is

now, we are interesting in the variable $y$, then, by "turning" the axles you have

then, if $y \in (0,1) \to x \in (0,y)$, and if $y \in (1,2) \to x \in (y-1,1)$. And finally, to found $f_Y(y)$ we need to split de interval.

Case 1 - $y \in (0,1)$: \begin{align*} f_Y(y) & = \int_{0}^{y}1 dx = y \end{align*} Case 2 - $y \in (1,2)$: \begin{align*} f_Y(y) & = \int_{y-1}^{1} 1 dx = 2-y \end{align*} Finally

$$ f_Y(y) = \begin{cases} y, & 0 <y < 1 \\ 2-y, & 1 < y < 2 \end{cases} $$

Answer 2

The safer way to do this may be to find the cdf $P(Y \le y)$ and then differentiate, but with your approach of $$f_Y(y)=\int_{-\infty}^{\infty} f_{X_1}(x_1) f_{X_2}(y-x_1) \, dx_1$$ with the supports of $X_1$ and $X_2$ restricted to $[0,1]$

• this is clearly $0$ when $y \lt 0$ and when $y \gt 2$
• when $0 \le y \le 1$ you would have $x_1>y$ requiring $x_2 < 0$, so it can be written as $$\int_{0}^y f_{X_1}(x_1) f_{X_2}(y-x_1) \, dx_1$$
• when $1 \le y \le 2$ you would have $x_1<y-1$ requiring $x_2 >1$, so it can be written as $$\int_{y-1}^1 f_{X_1}(x_1) f_{X_2}(y-x_1) \, dx_1$$

which you can combine as $$f_Y(y)= \int_{\max(0, y-1)}^{\min(1,y)} f_{X_1}(x_1) f_{X_2}(y-x_1) \, dx_1.$$

Since you have two uniform distributions, this is $\min(1,y)-\max(0, y-1)= |y-1|$ when $0 \le y \le 2$.

Answer 3

Changing notation slightly, for all choices of fixed real number $z$, \begin{align}f_Z(z) = f_{X+Y}(z) &= \int_{-\infty}^\infty f_X(x)f_Y(z-x) \, \mathrm dx\\ &= \int_{0}^1 f_X(x)f_Y(z-x) \, \mathrm dx & \text{since }f_X(x) = 0 \text{ when }x\notin [0,1]\\ &= \int_{0}^1 f_Y(z-x) \, \mathrm dx & \text{since }f_X(x) = 1 \text{ when }x\in [0,1]. \end{align} Consider $4$ different possibilities for the fixed number $z$:

Case 1: $z < 0$. As $x$ increases from $0$ to $1$, the value of the argument $z-x$ of the integrand $f_Y(z-x)$ is always less than $0$, and so the integrand is $0$ for all $x\in [0,1]$. Conclusion: $f_Z(z) = 0$ when $z < 0$.

Case 2: $z > 2$. As $x$ increases from $0$ to $1$, the value of the argument $z-x$ of the integrand $f_Y(z-x)$ is always greater than $1$, and so the integrand is $0$ for all $x\in [0,1]$. Conclusion: $f_Z(z) = 0$ when $z > 2$.

Case 3: $0 \leq z \leq 1$. Now, as $x$ increases from $0$ to $1$, the value of the argument $z-x$ of the integrand $f_Y(z-x)$ decreases from its initial value $z \in [0,1]$ when $x = 0$ to value $0$ when $x = z$ and goes negative as $x$ sweeps past $z$ on its way to $1$. Thus, the integrand has value $1$ only for $x\in [0,z]$. Conclusion: $f_Z(z) = z$ when $z \in [0,1].$

Case 4: $1 \leq z \leq 2$. Now, as $x$ increases from $0$ to $1$, the value of the argument $z-x$ of the integrand $f_Y(z-x)$ decreases from its initial value $z > 1$ when $x = 0$ to value $1$ when $x = z-1 \in [0,1]$ and continues to decrease to value $z-1 \in [0,1]$ when $x=1$. Thus, the integrand has value $1$ only for $x\in [z-1,1]$, an interval of length $1-(z-1) = 2-z$. Conclusion: $f_Z(z) = 2-z$ when $z \in [0,1].$