Three semicircles geometry problem from TikTok

Question

Here's a fun geometry problem I stumbled on TikTok. We are given the diameters of the red and yellow circles (which are tangent) and supposed to determine the diameter of the big circle.

It is easy to trace some triangles, apply Pythagoras and find similarities to achieve the solution of $x = 5$. Now what might've called your attention is that this is the sum of the diameters of the small circles. Having noticed that I ran to Geogebra and tested this configuration with several ratios of diameters for the red and yellow circles and incredibly enough this relation seems to be always true. Now I wonder why.

Yes, we can achieve this result the same way as before, by tracing triangles, applying Pythagoras and finding similarities, but this doesn't satisfy me. I think there is something more fundamental to this. Can we prove this another way? Perhaps by noticing there is a corner homothety between the red and outer circle?

It seems to me the yellow semicircle can 'slide through' the side of the red circle while still touching the outer circle with its corner until it fits perfectly on its diameter.

Answer 1

I think the semicircles are a bit misleading. Consider the following problem instead:

Say there are two circles, red and yellow, that touch each other. Say the yellow circle is to the right of the red circle initially. Let $C$ be the center of the yellow circle, and $P$ be the right-most point on the yellow circle. Now, move the yellow circle around the red circle while still touching it (don't rotate the yellow circle about its center). It's obvious that the locus of $C$ is a circle. But $P$ is just a fixed horizontal vector away from $C$, so the locus of $P$ is a circle too. In fact, it is precisely the bigger circle.

(animation by @Blue)

Answer 2

While the other answer gives a nice illustration of what is happening, it doesn't give a proof. The nicest proof I see is to use similarity in this way: The length of the chord $OP$ is equal to the sum of the lengths of the two chords that make it up, and each chord's length is proportional to the radius of its circle, and we're done.

More formally, let $r_1,r_2,r_3$ be the radii of the red, yellow, and outer (black) circles. Let the length of segment $OP$ be $z_3$. For $i=1,2,3$, we have $z_i = 2 r_i \sin(\phi/2)$, so $z_1 + z_2 = z_3$ implies $r_1 + r_2 = r_3$.

We never used tangency of the yellow circle to the black diameter. We only used these facts: the yellow and red circles are tangent, the location of $O$, and $P$ lies on the black semicircle at the "rightmost" point of the yellow circle. So the claim $r_1 + r_2 = r_3$ holds no matter where $P$ lies on the black semicircle. That's nicely illustrated in Blue's animation in the other answer.

One fun consequence of similarity is that red and blue paths to $P$ have equal length (namely $r_3 \phi$):

Answer 3

A "proof without words":

But since words do help clarify:

That the original diagram shows the yellow semicircle tangent to the bottom line is a red herring. We don't need that assumption.

We are given the red and green semicircles, and we know they are tangent and their diameters are parallel. Say the red semicircle has center $A$ and radius $a$, and the green semicircle has center $B$ and radius $b$. Let $C$ be the right endpoint of the green semicircle diameter. Construct point $D$ on the line through the red diameter, right of $A$ and with distance $AD = b$. Since $BC$ and $AD$ are parallel and have equal lengths, quadrilateral $ABCD$ is a parallelogram. Therefore $CD=AB=a+b$, and the circle centered at $D$ with radius $a+b$ passes through the left endpoint of the red diameter and through $C$.

Answer 4

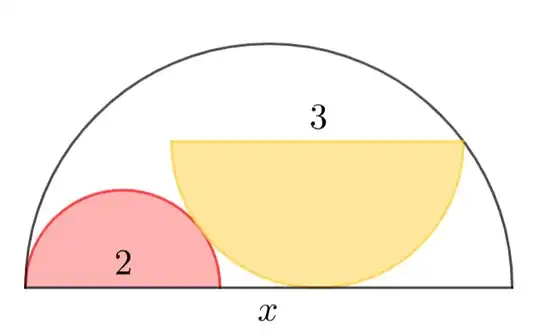
A more traditional and elaborate geometrical proof.

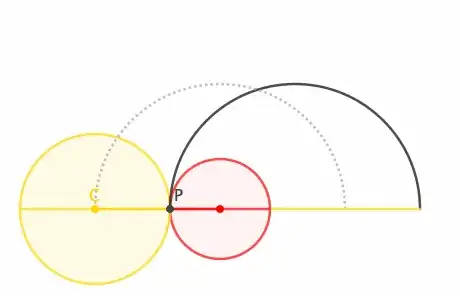
Let's look at the general situation for any pair of semi-circles $R_1$ and $R_2$ such that $R_1 < R_2$.

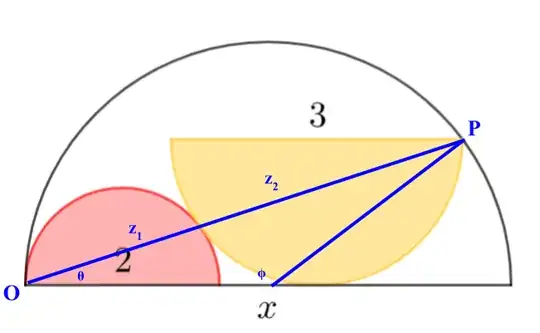
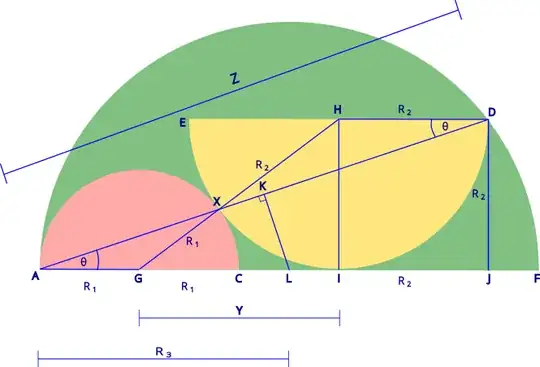
Consider $\triangle GHI$ and let $Y = |GI|$

By Pythagoras:

$$ Y = \sqrt{(R_1 + R_2)^2 - R_2^2} = \sqrt{R_1^2 + 2R_1R_2} \tag{ . . . 1}$$

Now observe that $|AD|$ is a chord of the enclosing semicircle of radius $R_3$.

As such, a perpendicular line from its mid-point $K$ onto the enclosing semi-circle's diameter $|AF|$ will intersect the latter at its center point $L$ so that $|AL| = R_3$.

Thus if $\;\; Z = |AD| \;\; $ and $\;\; \angle JAD = \theta \;\;$ we have

$$ Z = \sqrt {(R_1 + R_2 + Y)^2 + R_2^2)} \tag{ . . . 2} \\ \\$$

$$ \begin{align} R_3 &= \dfrac{\dfrac{Z}{2}}{\cos{\theta}} \\ \\ \text{Since} \;\;\;\; \cos \theta &= \dfrac{R_1 + Y + R_2}{Z} \\ \\ R_3 &= \dfrac{\dfrac{Z}{2}}{\dfrac{(R_1+R_2+Y)}{Z}} \\ \\ &= \dfrac{\dfrac{Z^2}{2}}{R_1+R_2+Y} \end{align} $$

Applying (2): $$ \begin{align} R_3 &= \dfrac{1}{2}\left[\dfrac{(R_1+R_2+Y)^2 + R_2^2}{R_1+R_2+Y}\right] \\ \\ &= \dfrac{1}{2}\left[R_1+R_2+Y + \dfrac{R_2^2}{R_1+R_2+Y}\right] \tag{ . . . 3} \end{align}$$

Noting that $$\begin{align} \dfrac{R_2^2}{R_1+R_2+Y} \; &= \; R_2^2 \; \left[\dfrac{1}{R_1+R_2+Y} \; . \; \dfrac{R_1+R_2-Y}{R_1+R_2-Y} \right] \\ \\ &= \; R_2^2 \; \left[\dfrac{R_1+R_2-Y}{(R_1+R_2)^2 - Y^2} \right] \end{align}$$

$$ $$

And since from (1): $ \;\; Y^2 = R_1^2 + 2R_1R_2 $

$$ $$

$$ \begin{align} \require{cancel} \implies \dfrac{R_2^2}{R_1+R_2+Y} \; &= \; \cancel{R_2^2} \; \left[\dfrac{R_1 + R_2 -Y}{\cancel{R_1^2} + \cancel{2R_1R_2} + \cancel{R_2^2} - \cancel{R_1^2} - \cancel{2R_1R_2}}\; \right] \\ \\ &= \; R_1+R_2-Y \tag{ . . . 4} \end{align}$$

Putting result (4) into expression (3):

$$ \require{cancel} R_3 = \dfrac{1}{2} \; \left[R_1 + R_2 + \cancel{Y} + R_1 + R_2 - \cancel{Y} \right] $$

So we finally have: $$ \boldsymbol{ {R_3 \; = \; R_1 \; + \; R_2} } \\ \\ $$

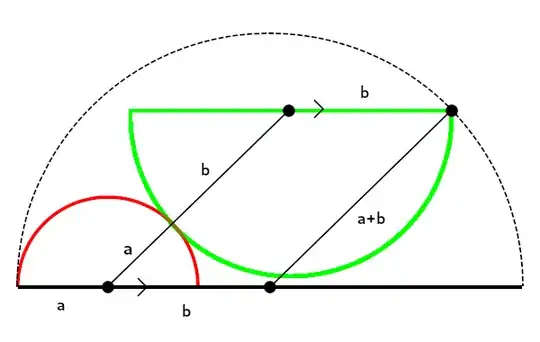
Alternative Easier Solution

Similar isosceles triangles $\triangle AGX$ and $\triangle DHX$:

$$ \begin{align} |AD| \; &= \; |AX| + |XD| \\ \\ |AD| \; &= \; 2R_1\cos{\theta} + 2R_2\cos{\theta} \\ \\ \; &= \; 2\cos{\theta}\;(R_1 + R_2) \\ \\ R_3 \; &= \; |AL| \\ \\ \; &= \; \dfrac{|AK|}{\cos{\theta}} \\ \\ |AK| \; &= \; \dfrac{|AD|}{2} \\ \\ \require{cancel} \text{Hence} \;\;\;\;\;\;\; R_3 \; &= \; \dfrac{\cancel{2\;\cos{\theta}}\;(R_1 + R_2)}{\cancel{2\;\cos{\theta}}} \\ \\ \text{Thus} \;\;\;\;\;\;\;\; \boldsymbol{ R_3}\; &= \; \boldsymbol{R_1 + R_2} \end{align} $$

$$ $$

As to the proof of the chord line $|AD|$ and the line joining the centers of the two semi-circles $|GH|$ meeting at the contact point, we can see from my diagram that this must be the case as $\triangle AGX $ and $\triangle DHX $ are similar triangles with ratio of their sides of $R_1:R_2$.

It seems to me that this ratio may only be maintained if $|GX| = R_1$ and $|HX| = R_2$ - which of course means that $|AD|$ goes through the tangent point of the semi-circles.

The curious thing for me is that having the larger semi-circle wide side up doesn't save space over having it wide side down. The answer from Pranay only partly satisfies me on this. It might be better to simulate a rotation of the larger semi-circle about a horizontal axis through the contact point. After $90^\circ$ of turning more horizontal space will be needed by the larger semi-circle since its wider part is now bearing upon the smaller semi-circle.

This reminds me of how both flank pieces of a shoe pattern are not too different in size despite the clear difference in the shape of the two sides of a shoe last. For centuries this fact was exploited by shoe factories: they got a sort of graphical average of the two patterns (the so-called mean forme) and exploited the stretchiness of leather to make up the differences. This process also allowed them to only need a single pressing die to click out right and left flank-pieces from a hide for each shoe-style/size combination - a significant saving in tooling costs. Nowadays laser-guided contour blades cut shoe patterns from a hide but looking at shoes the actual patterns seem to be designed the same old way !

In the case above, the two semi-circle arrangements are precisely wrapped by the same enclosing semi-circle. This makes me wonder if such an idea could be exploited in designing precision engineered things like gears or bearings - things not yet obsolete due to advances in nanomechanical and biomechanical systems.