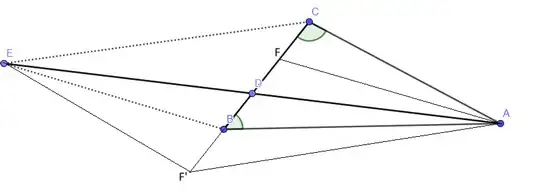
I am trying to isolate a geometric, synthetic version of the stated property in the following Lemma. It turns out that the point $A$ has a secondary meaning, and can be eliminated, all the information about $A$ is also covered by $E$. The Lemma constructs instead of the triangle $\Delta ABC$ its reflection w.r.t. $D$, which is a triangle $\Delta EPQ$ with the same properties, the angle in $P$ is half the angle in $Q$. We denote by $x$ this angle. The stated property is then a corollary of the Lemma, and it is explained in natural manner using geometric constructions. Many properties of the involved points are listed and proved. I tried hard to obtain a purely synthetic proof of the Lemma, but complications occur on the path. So there will be also a trigonometry piece, involving the theorem of sines, cosines (Pythagoras generalized), and straightforward trigonometric calculus.
Lemma: Consider on the line the five points $Q,B,D,P,C$ in this order, so that the segments between two consecutive points have same length $QB=BD=DP=PC$.
$(a)$ Let $Y$ be the common mid point of the segments $BD$, $QP$, and denote by $\pi_Y$ thir common perpendicular bisector.
Let $X$ be a point on $\pi_Y$. Denote by $x$ the (measure of the) equal angles $x=\widehat{XPQ}=\widehat{XQP}$.
$(b)$ Let $E$ be the point on the ray $[PX$ so that the angle in $Q$ in $\Delta EPQ$ is $2x$. Let $A$ be the reflection of $E$ w.r.t. $D$. So both triangles $\Delta EPQ$, $\Delta ABC$ have the angles in order $180^\circ-3x$, $x$, $2x$.
$(c)$ Let $M$ be the mid point of the segments $BC$ and $DP$, and let $\pi_M$ be their common perpendicular bisector. Let $S$ be the intersection of $\pi_M$ with $XP$.
$(d)$ On $\pi_B$, the perpendicular in $B$ on the line $QBDPC$, consider $T$ on the same side as $X,S$ so that $BT=2MS$. Then $T$ is the incenter of $\Delta ECQ$, and $ET,CST,QT$ are the angle bisectors of this triangle.
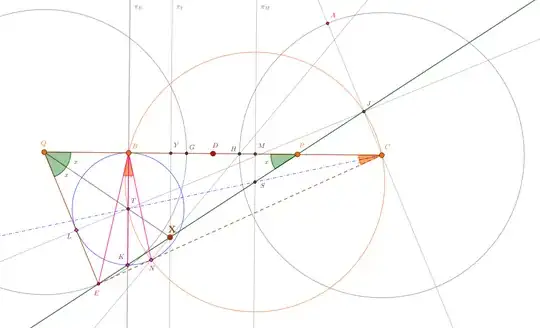
$(e)$ Let $L\in QE$, $N\in CE$ be the other two tangent points of the incircle $\odot (T)$ on the corresponding sides. (The third one is $B$.) Let $K$ be on $\pi_B$, on the ray $[BT$, with $BK=2BT$. Then $K$ is also on this incircle, and also on the line $EXSP$. Let $J$ be on $[CA$ so that
$\Delta SCJ$ is isosceles in $S$ (with two angles of $2x$ in $C,J$). Then $SJ=SC=SN=ST=SB$, i.e. $J,C,N,T,B$ are on the same circle centered in $S$, and $L,T,J$ are collinear. Also: the triangles are similar: $\Delta TBE\sim\Delta SCE$. Let $G,H$ be in the segment $QC$ be so that $QE=QG=HC$. (The points $G,H$ are reflected in each other w.r.t. $D$.)
Then $N,X,H$ are collinear. The lines $QX$, $EG$, $BN$ are concurrent in a point of the circle $\odot(TLEN)$.
$(f)$ Then finally the following angles have the same measure, denote it by $y$:
$$
y
=\widehat{EBT}
=\widehat{TBN}
=\widehat{BCT}
=\widehat{TCN}
\ .
$$
This implies the wanted relation:
$$
2\widehat{EBC}
=2\left(\widehat{EBT}
+\widehat{TBC}\right)
= 2(y+90^\circ)
=2y+180^\circ
=
\widehat{BCE}
+180^\circ\ .
$$
Proof of the Lemma: In $(a)$, $(b)$, $(c)$ there is nothing to be shown, these items are dealing with construction of points.
We show the property in $(d)$ of $T$, claimed to be the incenter of $\Delta ECQ$.
The angles of $\Delta EPQ$ are $180^\circ-3x$, $x$, $2x$, so by the theorem of sines, after rescaling, we may and do take them to be $PQ=6\sin(180^\circ-3x)=6\sin 3x$, $EP=6\sin 2x$, $EQ=6\sin x$, so that each segment among $QB,BD,DP,PC$ is $2\sin 3x$, and $PM=\sin 3x$. We compute the area $[ECQ]$ of triangle $\Delta ECQ$, then its (half-)perimeter, then its inradius $r$ as the quotient. It is convenient to use $s=\sin x$ below, and force polynomial expressions in $s$ when possible.
When not, we may also use $c=\cos x$.
$$
\begin{aligned}{}
[ECQ]
&=\frac 12 QE\cdot QC\cdot \sin \hat Q
= \frac 12 6\sin x\; 8\sin3x\; \sin 2x
\\
&= 24\; \sin x\; \sin 2x\; \sin 3x=48s^3c(3-4s^2)
\ .
\\[3mm]
CE^2 &= PE^2+PC^2-2\;PE\cdot PC\cdot\cos \hat P\\
&=36\sin^2 2x+4\sin^2 3x + 2\cdot 6\sin 2x\cdot 2\sin 3x\; \cos x\\
&=144\sin^2x\cos^2x + 4\sin^2x(3-4\sin^2 x)^2 + 48\sin^2x\cos^2x(3-4\sin^2x)\\
&=144s^2(1-s^2) + 4s^2(3-4s^2)^2 + 48s^2(1-s^2)(3-4s^2)\\
&=4s^2(9-8s^2)^2\ ,\\
CE &= 2s(9-8s^2)=2\sin x(9-8\sin^2x)\ ,
\\[3mm]
\operatorname{Perimeter}(ECQ)
&=CQ+EQ+EC\\
&=8\sin 3x + 6\sin x + 2\sin x(9-8\sin^2x)\\
&=8s(3-4s^2) + 6s
+2s(9-8s^2)=48s(1-s^2)=48sc^2
\\[3mm]
r&=\frac{48s^3c(3-4s^2)}{24sc^2}=2\cdot\frac sc\cdot s(3-4s^2)
=2\tan x\cdot\sin 3x
\\
&=2\tan x\cdot MP=2MS=BT\ .
\end{aligned}
$$
So $T$ is the point on the angle bisector in $Q$ of $\Delta ECQ$, and its distance to $CQ$ is exactly $r$, the inradius. So $T$ is the incenter of this triangle. We note that $C,S,T$ are collinear because of $BT:MS=2:1=BC:MC$.
We come to $(e)$.
Since $KB\perp CQ$, and the incenter $T$ is the mid point of $KB$, this segment is a diameter. We have $BK: MS=4:1=BP:MP$, so $K,S,P$ are colinear.
We compare $\Delta TBC$, $\Delta TNC$. From $TB=r=TN$, right angles in $B,N$, and the common $CT$ we see their congruence.
(Note that $S$ is the mid point of their hypotenuses.)
So $CN=CB$, and from here $\Delta CSB$, $\Delta CSN$ are congruent.
We obtain so far $SB=ST=SN=SC$. In particular, $BTNC$ is cyclic, so there is a common value $y$ for the angles:
$$
y = \widehat{TBN}= \widehat{TCN}= \widehat{BCT}.
$$
We need one more angle in the list, the other angle $\widehat{EBT}$ in $B$.
For this, i could find only a similarity argument. We show that the triangles $\Delta TBE$ and $\Delta SCE$ are similar. The angle in $T$ in the first one is $\hat T =\widehat{ETQ}+\widehat{QTB}=(90^\circ +y)+(90^\circ -x)
=180^\circ -x+y$. The same angle is in $S$ in the second triangle, $
\hat S=180^\circ-\widehat{CSP}=
180^\circ-(\widehat{MPS}-\widehat{MCS})=180^\circ-(x-y)$.
We need a proportionality. For this we compute:
$$
\begin{aligned}
\frac{TB}{SC}
&=
\frac{TB}{SB}
=\frac{\sin\widehat {BST}}{\sin\widehat {BTS}}
=\frac{\sin 2y}{\sin(90^\circ-y)}
=\frac{\sin 2y}{\cos y}
\\
&=2\sin y=\frac{2MS}{SC}\ ,\\
\frac{TE}{SE}
&
=\frac{\sin\widehat {TSE}}{\sin\widehat {ETS}}
=\frac{\sin\widehat {TSE}}{\sin\widehat {ETC}}
=\frac{\sin (x-y)}{\sin(90^\circ+x)}
\\
&=
\frac{\sin (x-y)}{\cos x}
=
\frac{\sin (x-y)}{\sin y}\cdot
\frac{\sin y}{\cos x}
=
\frac{PC}{\color{gray}{PS}}\cdot\frac{MS/SC}{MP/\color{gray}{PS}}
\\
&=\frac{PC}{MP}\cdot \frac{MS}{SC}=\frac{2MS}{SC}\ .
\end{aligned}
$$
This shows the wanted similarity.
In particular, the angle $\hat B$ in $\Delta TBE$ is the same one as $y=\hat C$ in $\Delta SCE$.
This shows $(f)$.
Note: At this point the OP property is shown.
We continue with the other "bonus" properties from $(e)$. (Maybe a geometric solution can be given using the one or the other property.)
Why are $L,T,J$ collinear? The lines $CJA$ and $QLE$ are parallel. (The pairs $Q,C$, $E,A$ are reflected in $D$.) We have $TL\perp QE$, so it is enough to show $TJ\perp AC$. We have $ST=SC=SJ$, $\Delta TJC$ is inscribed in a half-circle, so $\hat J=90^\circ$ in this triangle.
We show the concurrence of $QX,EG,BN$. Let $U$ be the projection of $Q$ on $EG$ in the isosceles $\Delta QEG$. Then by construction $U= EG\cap QX$.
Because of the right angles in $L,U$ the quadrilateral $UTLE$
is cyclic, the circumcircle having $TE$ as diameter. We can add $N$ since it is also on this circle. Then
$$
\widehat{TUN}=
180^\circ-\widehat{NLT}
=90^\circ+\widehat{NLE}
=90^\circ+\frac 12(180^\circ-\hat E)
=90^\circ+(x+y)\ ,
\\
\widehat{TUB}
=\widehat{QUB}
=180^\circ-\hat Q-\hat B
=180^\circ-x-(90^\circ+y)
=90^\circ-(x+y)\ ,
$$
and these angles add to $180^\circ$, so the points $B,U,N$ are collinear.
The remained collinearity of $N,X,H$ is done by computation.