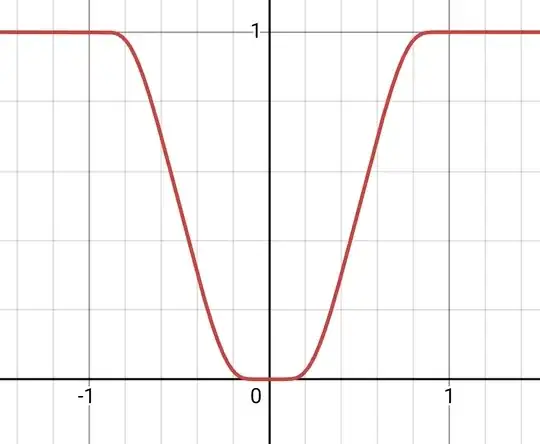
I want to regularize a function such that $G_{\epsilon}(x) = 1$ for $|x| > \epsilon$, where $\epsilon > 0$ is small, and $G_{\epsilon}(0) = 0$, so that $G_{\epsilon}$ converges uniformly towards 1.
The function I tried is the following: $$ F_{\epsilon}(x) = \left|\tanh\left(\frac{x}{\epsilon}\right)\right| $$ but even after trying to regularize the absolute value function using $x \tanh\left(\frac{x}{\epsilon}\right)$, I am not able to get a good approximation for $G_{\epsilon}$.
As @totaldependentrandomchoice note in his comment, you could try by scalling some smooth bump function and subtracted from one.
As example, you could use some argument $f(\frac{x}{\epsilon})$ for the following function with $k>0$:
$$f(x,k) = \begin{cases} 1,\quad x\leq -1;\\ 1,\quad x\geq 1;\\ 0,\quad x=0;\\ \dfrac{1}{1+\exp\left(\frac{-k(1-2|x|)}{x^2-|x|}\right)},\quad\text{otherwise;} \end{cases}$$
You could check it in Desmos. Note that $f(x)$ is smooth class $C^\infty$, but is not analytic in $x=\{-1,\ 0,\ 1\}$. Also in this case, if you use $k<0$, you will recover the smooth bump function from here.
