4

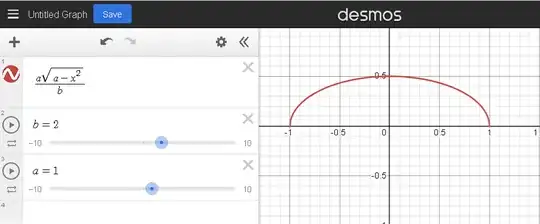
I need help with solving this integral:

$$L =\int_0^a\sqrt{1+\left(\frac{ax}{b\sqrt{a^2-x^2}}\right)^2}\;dx $$

I am trying to use this integral to find a function that will give an Approximation to the circumference of an ellipse, I am not sure if what I am doing is correct so please tell me if you see that the logic that I am using is false

I used the function of an ellipse which is the one you see below

enter image description here

Then I used this function which is supposed to find the arc length of a function

$$L =\int_a^b\sqrt{1+\left(\frac{dy}{dx}\right)^2}\;dx $$

So what I did was found the derivative of the ellipse function and then plugged it into the arc length function but what was left to do was solve the integral of the arc length function to find what I think will be the rule for the circumference of an ellipse witch is the one you see in the top

Blue
  • 83,939
Mustafa Abdullah
  • 89

1 Answers1

6

Using the substitution $x=a\sin \theta$ as Claude Leibovici suggested, we can transform the integral into an elliptic integral. $$ \begin{aligned} L & =\int_0^{\frac{\pi}{2}} \sqrt{1+\frac{a^4 \sin ^2 \theta}{b^2 \cdot a^2 \cos ^2 \theta}} \cdot a \cos \theta d \theta \\ & =\frac{a^2}{b} \int_0^{\frac{\pi}{2}} \sqrt{b^2 \cos ^2 \theta+a^2 \sin ^2 \theta} d \theta \\ & =\frac{a}{b} \int_0^{\frac{\pi}{2}} \sqrt{b^2+\left(a^2-b^2\right) \sin ^2 \theta} d \theta \\ & =a \int_0^ \frac{\pi}{2}\sqrt{1-\left(1-\left(\frac{a}{b}\right)^2\right) \sin ^2 \theta} d \theta \\ & =a E\left(1-\left(\frac{a}{b}\right)^2\right) \end{aligned} $$ where $E(k^2)$ is an Elliptic integral.

Lai
  • 31,615