Number of ways the frog moves from A to B

Question

A frog is travelling from point A (0,0) to point B (5,4) but each step can only be 1 unit up or 1 unit to the right. Also, the frog refuses to move three steps in the same direction consecutively. Compute the number of ways the frog can move from A to B.

I solved this question as per the method suggested by user2661923 in this post, and came up with the following solution:

$ P5 $(Ups):

$a_1: 2-2-1$

$b_1: 2-1-1-1$

$c_1: 1-1-1-1-1$

$ P4 $(Rights):

$a_2: 2-2$

$b_2: 2-1-1$

$c_2: 1-1-1-1$

Working the cases:

$ a_1:a_2 = 1 \times 3 = 3$

$ a_1:b_2 = 2 \times 3 \times 3 = 18$

$ a_1:c_2 = 1 \times 3 = 3 $

$ b_1:b_2 = 1 \times 4 \times 3 = 12$

$ b_1:c_2 = 2 \times 4 = 8$

$ c_1:c_2 = 1$

Therefore, the total number of ways: $ 3 + 18 + 3 + 12 + 8 + 1 = 45$

Is this correct?

I think not. The generating function approach in the linked question suggests to me a number slightly higher than $42$. — Henry, Oct 08 '24 at 05:09
Oh yes, I forgot to consider the case, $a_1$ and $c_2$. It still seems quite small right? Am I missing any other case(s)? — Shs Tht, Oct 08 '24 at 05:31

Henry · Accepted Answer · 2024-10-08T05:44:15.740

Yes. Your corrected $45$ seems to be correct.

Using the generating function approach mentioned in another reply to the same linked question and Maxima,

taylor(taylor(1/(1-x-y+x^3/(1+x+x^2)+y^3/(1+y+y^2)), x, 0, 6), y, 0, 6);

gives

(208*x^6+113*x^5+43*x^4+10*x^3+x^2+...)*y^6+ 
(113*x^6+84*x^5+45*x^4+16*x^3+3*x^2+...)*y^5+
(43*x^6+45*x^5+34*x^4+18*x^3+6*x^2+x+...)*y^4+
(10*x^6+16*x^5+18*x^4+14*x^3+7*x^2+*x+...)*y^3+
(x^6+3*x^5+6*x^4+7*x^3+6*x^2+3*x+1+...)*y^2+
(x^4+2*x^3+3*x^2+2*x+1+...)*y+
(1+x+x^2+...)+...

and you can see that the coefficient of $x^5y^4$ (and also of $x^4y^5$) is $45$.

Or as a manual recursive attempt, this counts the number of ways to each vertex: in red if the last move was horizontal and in blue if the last move was vertical, with $29+16=45$.

score 1 · Answer 2 · answered Oct 08 '24 at 07:55

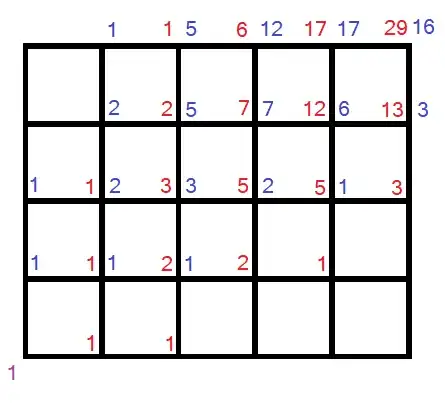
going up by 1 step: $u$ going right by 1 step: $v$

possibilities for 5 ups with right movements removed: $(u,u) \implies$ 2 consecutive ups and $(u) \implies $ 1 up isolated:

$(u),(u,u),(u,u)$ or

$(u),(u),(u),(u,u)$ or

$(u),(u),(u),(u),(u)$

possibilities for 4 rights is similar.

$(r,r),(r,r)$ or

$(r),(r),(r,r)$ or

$(r),(r),(r),(r)$

Case 1:

For $(u),(u,u),(u,u)$ the possibilities for rights is :

$(r,r),(r,r)$ (gives 1 possibilities with above u's for each order of $(u),(u,u),(u,u)$) or $(r),(r),(r,r)$ (gives 6 possibilities with above u's for each ordering of $(u),(u,u),(u,u)$) or $(r),(r),(r),(r)$ (gives 1 possibilities with above u's for each ordering of $(u),(u,u),(u,u)$)

So 8 possible r's are present for above defined u's: $(u),(u,u),(u,u)$. there are 3 ways of arranging this u's. So $8 \times 3 = 24$ ways.

Case 2:

For $(u),(u),(u),(u,u)$ the possibilities for rights is :

$(r,r),(r,r)$ (gives 0 possibilities with above u's for each order of $(u),(u),(u),(u,u)$) or $(r),(r),(r,r)$ (gives 3 possibilities with above u's for each ordering of $(u),(u),(u),(u,u)$) or $(r),(r),(r),(r)$ (gives 2 possibilities with above u's for each ordering of $(u),(u),(u),(u,u)$)

So 5 possible r's are present for above defined u's: $(u),(u),(u),(u,u)$. there are 3 ways of arranging this u's. So $5 \times 4 = 20$ ways.

Case 3:

For $(u),(u),(u),(u),(u)$ the possibilities for rights is :

$(r,r),(r,r)$ (gives 0 possibilities with above u's for each order of $(u),(u),(u),(u),(u)$) or $(r),(r),(r,r)$ (gives 0 possibilities with above u's for each ordering of $(u),(u),(u),(u),(u)$) or $(r),(r),(r),(r)$ (gives 1 possibilities with above u's for each ordering of $(u),(u),(u),(u),(u)$)

So 1 possible r's are present for above defined u's: $(u),(u,u),(u,u)$. there are 1 ways of arranging this u's. So $1 \times 1 = 1$ ways.

Case 1: 24 ways + Case 2: 20 ways + Case 3: 1 way = 45 ways.

score 1 · Answer 3 · answered Nov 26 '24 at 02:54

A frog is travelling from point A (0,0) to point B (5,4) but each step can only be 1 unit up or 1 unit to the right. Also, the frog refuses to move three steps in the same direction consecutively. Compute the number of ways the frog can move from A to B.

I just added a 2nd answer to this previous question.

I will use the same methodology and syntax from my 2nd answer to the previous question to attack this question. In effect, you have $~n = 5, ~k = 4.$

The desired enumeration is the number of solutions to

$x_1 + x_2 + \cdots + x_5 = 5.$
$x_1, ~x_2, ~\cdots, ~x_5 \in \{0,1,2\}.$
For $~i \in \{2, 3\},~$ you can not have
$x_i = 0 = x_{i+1}.$

Assume that exactly $~r~$ of the variables $~x_2, ~x_3, ~x_4~$ are forced to equal $~0,~$ and that the $~(3-r)~$ other variables from $~x_2, ~x_3, ~x_4~$ are forced to be $~\geq 1.$

Then, $~r~$ must be some element in $~\{0,1,2\}.$

The numbers are small enough that $~f(n,k,r) = f(5,4,r)~$ can be calculated at a glance.

$$f(5,4,0) = 1, ~f(5,4,1) = 3, ~f(5,4,2) = 1.$$

Then $~g(n,k,r) = g(5,4,r),~$ which becomes the enumeration of the number of solutions to

$x_1 + x_2 + \cdots + x_{5-r} = r + 2.$
$x_1, ~x_{5-r} \in \{0,1,2\}.$
$x_{2}, ~\cdots, ~x_{4-r} \in \{0,1\}.$

So, by manual inspection,

$$g(5,4,0) = 12, ~g(5,4,1) = 10, ~g(5,4,2) = 3.$$

Therefore, the final enumeration is

$$\sum_{r = 0}^2 [ ~f(5,4,r) \times ~g(5,4,r) ~]$$

$$= [ ~1 \times 12~] + [ ~3 \times 10~] + [ ~1 \times 3~] = 45.$$

Number of ways the frog moves from A to B

3 Answers3

Linked