I had just searched a lot about it, and found a way with locus(Braikenridge-Maclaurin Theorem or conversed-Pascal’s Theorem) and with equation(determinant), couldn't I get any proof with just a “construction.”
How do I draw a conic section without using a locus that passes given 5 distinct points? Is it possible, at least?
Just for more context, I’ll add two ways I found, which can be easily seen in others’ posts.
Way 1. By Locus
For given point A, B, C, D, E, we can draw some lines:
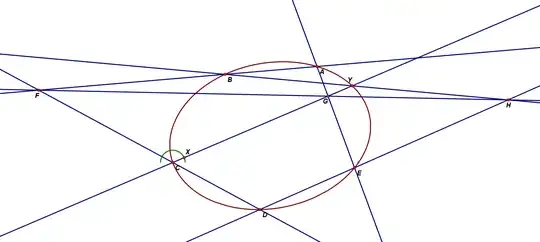\begin{align}
1. \; & AB \; \cap \; CD = F. \\
2. \; & X: \text{arbitrary point on a semicircle with its center $C$.} \\
3. \; & CX \; \cap \; AE = G. \\
4. \; & FG \; \cap \; DE = H. \\
5. \; & BH \; \cap \; CG = Y. \\
6. \; & \text{Draw a locus of $Y$, which forms a conic section by Braikenridge-Maclaurin Thm.} \blacksquare
\end{align}
Way 2. By Determinant of Matrix
Since all of the conic sections can be expressed as $Ax^2+Bxy+Cy^2+Dx+Ey+F=0$, we can state a matrix equation with given 5 points $P_i(x_i, y_i), i=1\text{~}5$ as:
$$ \begin{bmatrix} x_1^2 & x_1y_1 & y_1^2 & x_1 & y_1 & 1 \\ x_2^2 & x_2y_2 & y_2^2 & x_2 & y_2 & 1 \\ x_3^2 & x_3y_3 & y_3^2 & x_3 & y_3 & 1 \\ x_4^2 & x_4y_4 & y_4^2 & x_4 & y_4 & 1 \\ x_5^2 & x_5y_5 & y_5^2 & x_5 & y_5 & 1 \end{bmatrix} \cdot (A, B, C, D, E, F)^T = 0. $$
Again, we can solve the equation as: $$ \det \begin{bmatrix} x_1^2 & x_1y_1 & y_1^2 & x_1 & y_1 & 1 \\ x_2^2 & x_2y_2 & y_2^2 & x_2 & y_2 & 1 \\ x_3^2 & x_3y_3 & y_3^2 & x_3 & y_3 & 1 \\ x_4^2 & x_4y_4 & y_4^2 & x_4 & y_4 & 1 \\ x_5^2 & x_5y_5 & y_5^2 & x_5 & y_5 & 1 \end{bmatrix} = 0. \blacksquare $$
