Geometric Interpretation of why row/column elementary operation doesn't change determinant?
I found this comment, which might potentially answer the question, but I'm not sure how to interpret it.
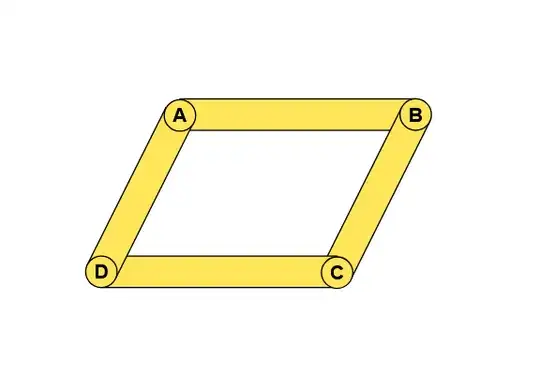
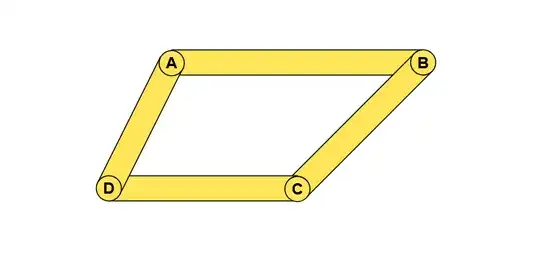
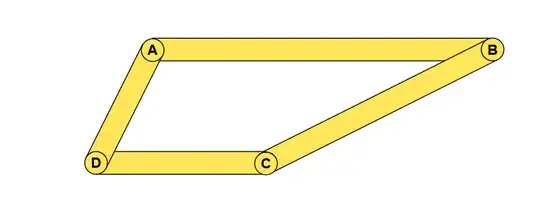
where CD is taken to be $v_1$ and BC is taken to be $v_2$, scaling it by dragging point B and leaving the other points unchanged transforms $v_2$ to $v_2 + λv_1$, where $λ$ is a constant. the comment seems to imply that the area of the geometric figures in all my images will be equivalent, but it doesn't look the same to me... Especially since if we rotate the figure $180$ degrees, $AB$ can be taken as the base and it seems to have increased.
What am i doing wrongly? Any guidance is appreciated!