0

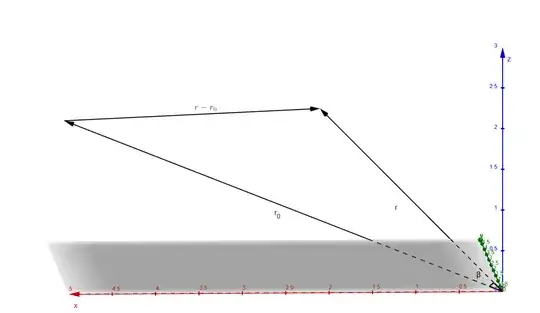
enter image description here

The 3D angle between two 3D vectors is $$\beta = \arccos\Big(\frac{\textbf{r}\cdot \textbf{r}_0}{|\textbf{r}||\textbf{r}_0|}\Big)$$, is there a way to get the 2D angles between the vector $\textbf{r}-\textbf{r}_0$? and the x-axis to get $\theta$ and the z-axis to get $\phi$?

Introducing the motivation of the problem, I need to integrate the following:

$$\int_0^{2\pi}\int_0^{\pi} \frac{\sin\phi}{|\textbf{r}-\textbf{r}_0|} d\phi d\theta$$

where $\theta$ is the azimuthal angle, and $\phi$ is the polar angle (from the z-axis) and we're in spherical coordinates; expanding the vector form into its vector form is $|\textbf{r}-\textbf{r}_0|^2 = (\textbf{r}-\textbf{r}_0)\cdot (\textbf{r}-\textbf{r}_0) = r^2 + r_0^2 - 2rr_0\cos\beta$. I need the $\theta$ and $\phi$ parts, I cannot just integrate $\beta$. Is there a formula that relates the 2D angles $\theta$ and $\phi$, and the 3D angle $\beta$ so that this integrand can now be integrable?

So I found the answer HERE

and I tested this formula out to verify it in Geogebra for some 2 vectors in 3D space and it works.

enter image description here

You can see that the distance $|\textbf{r}-\textbf{r}_0|$ computed in $b = \sqrt{|\textbf{r}|^2+\textbf{r}_0^2-2\textbf{r}\textbf{r}_0\cos\beta}$ is the same as that in distance d which uses: $$\cos\beta = \sin\phi\sin\phi_0\cos(\theta - \theta_0) +\cos\phi\cos\phi_0$$

Researcher R
  • 807
  • Same formula, take the dot product with unit vectors along the $x$ and $z$ axes. – Paul Sep 20 '24 at 06:53
  • First of all the angle between 2 vectors is a 2D angle. What is called a solid angle is how a surface is seen from a point and is measured in steradians. – Serge Ballesta Sep 20 '24 at 07:15
  • @Paul I realize now my question isn't quite formed right. $$\theta = \arccos\Big(\frac{(\textbf{r}-\textbf{r}_0)\cdot \hat{\textbf{i}}}{|\textbf{r}-\textbf{r}_0||\hat{\textbf{i}}|}\Big),\phi = \arccos\Big(\frac{(\textbf{r}-\textbf{r}_0)\cdot \hat{\textbf{k}}}{|\textbf{r}-\textbf{r}_0||\hat{\textbf{k}}|}\Big) $$. What I'm going to need is a way to rewrite $\cos(\beta)$ in terms of $\theta$ and $\phi$ – Researcher R Sep 20 '24 at 21:25
  • @SergeBallesta So a 2D angle in 3D space then? – Researcher R Sep 20 '24 at 22:30

1 Answers1

1

What you're asking for is $$|\boldsymbol r-\boldsymbol r_0|=r^2+r_0^2-2rr_0\,\hat{\boldsymbol r}\cdot\hat{\boldsymbol r}_0,$$ where $$\hat{\boldsymbol r}\cdot\hat{\boldsymbol r}_0=\cos\gamma=\cos\theta\cos\theta_0+\sin\theta\sin\theta_0\cos(\phi-\phi_0)$$ is the spherical version of the law of cosines.

This frequently appears in observational astronomy (in many coordinate systems) and when expanding the $3$D Green's function (as I already mentioned to you some time): $$\frac{1}{|\boldsymbol r-\boldsymbol r_0|}=\sum_{\ell\ge 0}\frac{\min(r,r_0)^\ell}{\max(r,r_0)^{\ell+1}}P_\ell(\cos\gamma)$$

Hug de Roda
  • 4,060