2

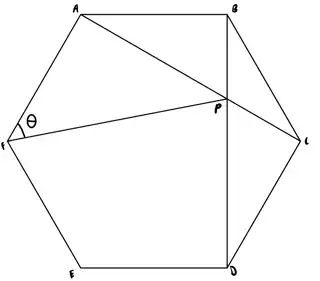
Hexagon ABCDEF with line AC and BD intersecting at P. What is the angle of AFP?

Hexagon ABCDEF with line AC and BD intersecting at P. What is the angle of AFP?

Hello, this is my first post on this forum, so apologies for all my poor formatting.

My question is this:

Is it possible to find $\theta$ using only simple geometry, ie. not trig?

It is simple to solve with trig, my solution below:

Note that $\angle BAP$ is $30^\circ$, and $\angle APB$ is $60^\circ$.

Thus let $AB=\sqrt{3}$. Note $AB=AF$.

It is clear from the classic $30^\circ$-$60^\circ$-$90^\circ$ triangle that $AP=2$.

And from triangle $AFP$ it is clear $\tan{\theta}=\frac{AP}{AF}=\frac{2}{\sqrt{3}} $

Therefore, $\theta=\arctan{\frac{2}{\sqrt{3}}}\approx 49.1^\circ$

This number appears to be irrational. Wolfram Alpha's continued fractions make me pretty sure of this. Does this mean the angle is impossible to find without trig? Is it provable that this cannot be found with only simple geometry?

Thanks, and sorry for my poor formatting :)

Henry
  • 169,616
Digby Wood
  • 31
  • 1
    The right-angled triangle $\triangle FAP$ has sides $\sqrt{3} : \sqrt{4} : \sqrt{7}$, so the sine, cosine and tangent of your angle are the relatively simple $\sqrt{\frac47}, \sqrt{\frac37}, \sqrt{\frac43}$. But I do not see that needs a simple expression for the angle itself. Perhaps the $7$ might be useful in a proof. – Henry Sep 19 '24 at 12:07
  • How do you know that those angles are 30 and 60 degrees? – Nate Sep 20 '24 at 01:50
  • https://math.stackexchange.com/q/112938/35416 might help prove $\theta$ transcendental. Proving that something can't be found without trigonometry sounds like it needs to be specified more clearly. Do you want to provide a positive list of what operations are permitted. Or do you want to avoid relying on some axiom which is important for trigonometry? I don't think there is one you could use for that, trigonometry emerges from fairly basic axioms. – MvG Sep 20 '24 at 20:16

0 Answers0